在平面直角坐标系 中,点M(
中,点M( ,
, ),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与x轴、y轴的另一交点分别为点D,A(如图),连接AM点P是弧AB上的动点.
),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与x轴、y轴的另一交点分别为点D,A(如图),连接AM点P是弧AB上的动点.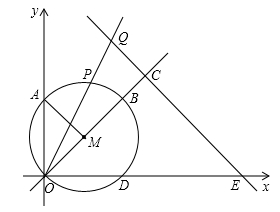
(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E.
①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S,求S与t的函数关系式及S的取值范围.
如图,已知扇形AOB中,∠AOB=120°,弦AB=2 ,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
(1)求弧AB的长;
(2)试判断∠ACB的大小是否随点M的运动而改变,若不变,请求出∠ACB的大小;若改变,请说明理由.
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形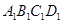 ,
,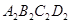 ,
,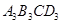 都是点A,B,C的外延矩形,矩形
都是点A,B,C的外延矩形,矩形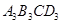 是点A,B,C的最佳外延矩形.
是点A,B,C的最佳外延矩形.
(1)如图1,已知A(-2,0),B(4,3),C(0,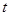 ).
).
①若 ,则点A,B,C的最佳外延矩形的面积为 ;
,则点A,B,C的最佳外延矩形的面积为 ;
②若点A,B,C的最佳外延矩形的面积为24,则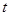 的值为 ;
的值为 ;
(2)如图2,已知点M(6,0),N(0,8).P(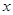 ,
,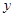 )是抛物线
)是抛物线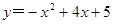 上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标
上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标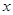 的取值范围;
的取值范围;
(3)如图3,已知点D(1,1).E(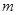 ,
,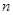 )是函数
)是函数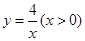 的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE= ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若AB=4,求FH的长(结果保留根号).
如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
(1)t为何值时,四边形APQD为矩形.
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC=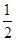 ,BC=
,BC=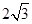 .
.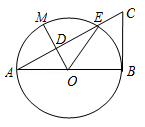
(1)求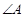 的度数;
的度数;
(2)求证:BC是⊙ 的切线;
的切线;
(3)求弧AM的长度.
(本题10分)如图,已知等边ΔABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线 DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.
(1)求证:DF⊥AC;
(2)若AB=8,求tan∠FGD的值.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
如图(1),抛物线 与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;
(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.
选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分。
题甲:如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.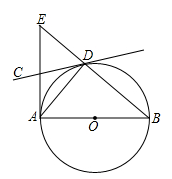
(1)求证:直线CD 是⊙O的切线;
(2)过点A作直线AB的垂线交BD的延长线于点E,且AB= ,BD=2,求S△ABE的面积
,BD=2,求S△ABE的面积
题乙:已知:一元二次方程x2﹣ax﹣3= 0
(1)求证:无论a取何值关于x的一元二次方程总有不等的实根。
(2)如果m,n是方程的两根且m2+n2=22试求a的值
如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.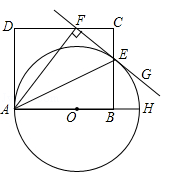
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
试题篮
()