初中数学圆幂定理解答题

如图，已知⊙的直径AB=12cm,AC是⊙的弦，过点C作⊙的切线交BA的延长线于点P，连接BC

（1）求证：∠PCA=∠B
（2）已知∠P=40°，点Q在优弧ABC上，从点A开始逆时针运动到点C停止（点Q与点C不重合），当△ABQ与△ABC的面积相等时，求动点Q所经过的弧长

（1）已知：如图1，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．
（2）如图2，AB切⊙O于点B，OA=2，∠OAB=30°，弦BC∥OA．求：劣弧BC的长．（结果保留π）

如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB．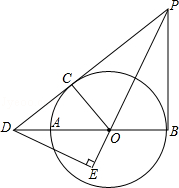

（1）求证：PB是的切线．
（2）若PB=6，DB=8，求⊙O的半径．

如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．

（1）将△ABC绕点B顺时针旋转90°得到△A′BC′，请画出△A′BC′；
（2）求BA边旋转到B A′位置时所扫过图形的面积．

如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0≤t≤2），连接PQ，以PQ为直径作⊙O．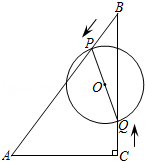

（1）当t=0.5时，求△BPQ的面积；
（2）设⊙O的面积为y，求y与t的函数解析式，并直接写出y的值最小时t的值；
（3）若⊙O与Rt△ABC的一条边相切，求t的值．

如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．

（1）请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C      、D       ；
②⊙D的半径=     （结果保留根号）；
③∠ADC的度数为    ．
④网格图中是否存在过点B的直线BE是⊙D的切线，如果没有，请说明理由；如果有，请直接写出直线BE的函数解析式。

已知：如图，AB是⊙O的直径，点C．D为圆上两点，且，CF⊥AB于点F，CE⊥AD的延长线于点E．

（1）试说明：DE＝BF；
（2）若∠DAB＝60°，AB＝8，求△ACD的面积．

已知：如图，等边△ABC内接于⊙O，点P是劣弧上的一点（端点除外），延长BP至D，使BD=AP，连接CD．

（1）若AP过圆心O，如图①，请你判断△PDC是什么三角形？并说明理由；
（2）若AP不过圆心O，如图②，△PDC又是什么三角形？为什么？

如图，AB是⊙O的直径，以OA为直径的⊙O₁与⊙O的弦AC相交于点D ，DE⊥OC于E。

（1）求证：AD=DC；
（2）求证：DE是⊙O₁的切线；
（3）如果OE=EC，请判断四边形O₁OED是什么四边形，并证明你的结论。

如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AE=弧 AB，BE分别交AD、AC于点F、G．

（1）判断△FAG的形状，并说明理由；
（2）若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由．

已知直线AB与轴、轴分别交于点A和点B，AB=10，且tan∠BAO=，以OA、OB为边作矩形OACB，点F 在BC上，过点F作AB的垂线，交AB于点D，交OA于点E，若⊙P是△AOB的内切圆，切点分别为M、N、G，

（1）求证：四边形PMON是正方形；
（2）求⊙P的半径;
（3）求当FE与⊙P相交的弦长为2．4时点F的坐标．

如图，AB为的直径，AB=AC，BC交于点D，AC交于点E．

（1）求证：BD=CD；
（2）若AB=8，∠BAC=45°，求阴影部分的面积．

七年级我们学过三角形的相关知识，在动手实践的过程中，发现了一个基本事实：
三角形的三条高（或三条高所在直线）相交于一点．
其实，有很多八年级、九年级的问题均可用此结论解决．
【运用】如图，已知：△ABC的高AD与高BE相交于点F，且∠ABC=45°，过点F作FG∥BC交AB于点G，求证：FG+CD=BD．

小方同学在解答此题时，利用了上述结论，她的方法如下：
连接CF并延长，交AB于点M，
∵△ABC的高AD与高BE相交于点F，
∴CM为△ABC的高．
（请你在下面的空白处完成小方的证明过程．）
【操作】如图AB是圆的直径，点C在圆内，请仅用无刻度的直尺画出△ABC中AB边上的高．

如图所示，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H．

（1）如果⊙O的半径为4，CD=，求∠BAC的度数；
（2）若点E为的中点，连接OE，CE．求证：CE平分∠OCD；
（3）在（1）的条件下，圆周上到直线AC距离为3的点有多少个？并说明理由．

以原点为圆心,为半径的圆分别交、轴的正半轴于A、B两点,点P的坐标为．
（1）如图一，动点Q从点B处出发，沿圆周按顺时针方向匀速运动一周,设经过的时间为秒，当时，直线PQ恰好与⊙O第一次相切，连接OQ．求此时点Q的运动速度（结果保留）；
（2）若点Q按照⑴中的方向和速度继续运动，
①当为何值时，以O、P、Q为顶点的三角形是直角三角形；
②在①的条件下，如果直线PQ与⊙O相交，请求出直线PQ被⊙O所截的弦长．