直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为()
A. |
B. |
C. |
D. |
如图,正方形ABCD的边长为2,点E在AB边上,四边形EFGB也为正方形,设△AFC的面积为S,则()
| A.S与BE长度有 | B.S=2.4 | C.S=4 | D.S=2 |
已知正比例函数y1=x,反比例函数y2=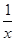 ,由y1,y2构造一个新函数y=x+
,由y1,y2构造一个新函数y=x+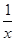 ,其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
,其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
①该函数的图象是中心对称图形;
②当x<0时,该函数在x=-1时取得最大值-2;
③y的值不可能为1;
④在每个象限内,函数值y随自变量x的增大而增大.
其中正确的命题是()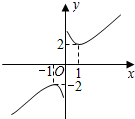
| A.①②④ | B.①②③ | C.②③ | D.①③ |
如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么()秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为 ,
, ,下列说法正确的是()
,下列说法正确的是()
| A.甲同学四次数学测试成绩的平均数是89分 |
| B.甲同学四次数学测试成绩的中位数是90分 |
| C.乙同学四次数学测试成绩的众数是80分 |
| D.乙同学四次数学测试成绩较稳定 |
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为()
| A.13 | B. |
C. |
D.12 |
下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为()
| A.135 | B.170 | C.209 | D.252 |
如图,菱形
的边长为
,
,以点
为圆心的圆与
相切,与
的延长线分别相交于点
,则图中阴影部分的面积为()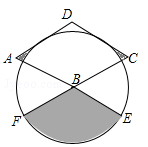
A.
B.
C.
D.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()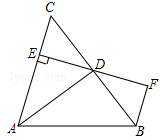
| A.4个 | B.3个 | C.2个 | D.1个 |
将正方形ABCD绕点A按逆时针方向旋转 ,得正方形
,得正方形 ,
, 交CD于点E,AB=
交CD于点E,AB= ,则四边形
,则四边形 的内切圆半径为().
的内切圆半径为().
A. |
B. |
C. |
D. |
如图,四边形ABCD中,∠C= ,∠B=∠D=
,∠B=∠D=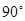 ,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为().
,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为().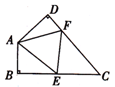
A. |
B.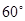 |
C. |
D.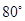 |
如图的四个转盘中,
.
转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是()
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为()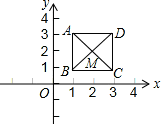
| A.(-2012,2) | B.(-2012,-2) | C.(-2013,-2) | D.(-2013,2) |
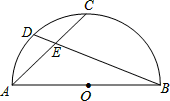
如图,AB是半圆O的直径,点C是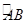 的中点,点D是
的中点,点D是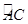 的中点,连接AC.BD交于点E,则
的中点,连接AC.BD交于点E,则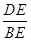 =()
=()
A.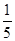 B.
B.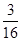 C.
C.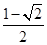 D.
D.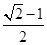
试题篮
()