如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的是( )
| A.点O1的坐标是(1,0) |
| B.点C1的坐标是(2,﹣1) |
| C.四边形OBA1B1是矩形 |
| D.若连接OC,则梯形OCA1B1的面积是3 |
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )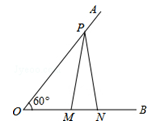
| A.3 | B.4 | C.5 | D.6 |
记 ,令
,令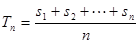 ,则称
,则称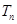 为
为 ,
, ,……,
,……, 这列数的“凯森和”.已知
这列数的“凯森和”.已知 ,
, ,……,
,……,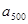 的“凯森和”为2004,那么13,
的“凯森和”为2004,那么13, ,
, ,……,
,……,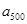 的“凯森和”为( )
的“凯森和”为( )
| A.2013 | B.2015 | C.2017 | D.2019 |
矩形ABCD中,边长AB=4,边BC=2,M、N分别是边BC、CD上的两个动点,且始终保持AM⊥MN.则CN的最大为( )
A.1 B. C.
C. D.2
D.2
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
A.12 B.9 C.4 D.6
D.6
定义一种运算: ,其中k是正整数,且k ≥2,[x]表示非
,其中k是正整数,且k ≥2,[x]表示非
负实数x的整数部分,例如[2.6]=2,[0.8]=0.若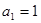 ,则
,则 的值为 ( )
的值为 ( )
| A.2015 | B.4 | C.2014 | D.5 |
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=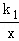 和y=
和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①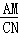 =
=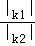 ; ②阴影部分面积是
; ②阴影部分面积是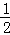 (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )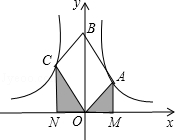
A.①②③ B.②④ C.①③④ D.①④
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.
①四边形A4B4C4D4是菱形;
②四边形A3B3C3D3是矩形;
③四边形A7B7C7D7周长为 ;
;
④四边形AnBnCnDn面积为 .
.
上述结论正确的是( )
| A.①②③ | B.②③④ | C.①③④ | D.①②③④ |
如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则△ABC的面积是 ( )
A.20 B.18 C.16 D.10
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
A.点A的左边
B.点A与点B之间
C.点B与点C之间
D.点B与点C之间或点C的右边
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数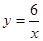 (x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
(x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )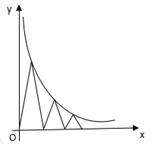
A.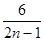 |
B.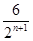 |
C. |
D.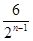 |
如图,直线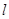 和双曲线
和双曲线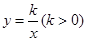 交于
交于 ,
, 两点,
两点,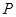 是线段
是线段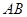 上的点(不与
上的点(不与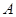 ,
,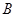 重合),过点
重合),过点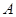 ,
,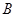 ,
,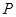 分别向
分别向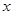 轴作垂线,垂足分别是
轴作垂线,垂足分别是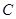 ,
, 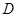 ,
,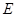 ,连接
,连接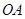 ,
,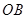 ,
,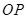 ,设
,设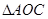 面积是
面积是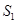 ,
,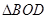 面积是
面积是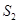 ,
,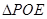 面积是
面积是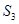 ,则( ).
,则( ).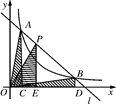
A.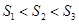 |
B.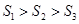 |
C.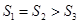 |
D. |
如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则tanC等于( )
A. B.
B. C.
C. D.
D.
如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
| A.1,2,3 | B.1,1,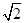 |
C.1,1,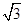 |
D.1,2,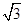 |
试题篮
()