初中数学解答题

如图，已知:EC=AC，∠BCE=∠DCA，∠A=∠E。求证：∠B=∠D．

钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航.渔政船接到报告后，立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.（假设渔船与渔政船沿同一航线航行）

（1）直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.]
（2）求渔船和渔政船相遇时，两船与钓鱼岛的距离.
（3）在渔政船驶往钓鱼岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

车间有工人85人，平均每人每天可以加工大齿轮16个或小齿轮10个，又知两个大齿轮与三个小齿轮配成一套，问应如何安排工人才能使生产的产品刚好成套？

.

如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．

（1）请完成如下操作：
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD．
（2）请在（1）的基础上，完成下列问题：
①写出点的坐标：C      、D        ；
②⊙D的半径=        .（ 结果保留根号）；
③若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面面积. （结果保留π）

(9分) 某校有A，B两个电脑教室，甲、乙、丙三名学生各自随机选择其中的一个电脑教室上课。求甲、乙、丙三名学生在同一个电脑教室上课的概率．（请在“树状图法”或“列表法”中选择合适的方法进行解答）

如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，求电视塔的高ED。

（本题每小题8分，共16分）
（1）（x+1）²=2                     
（2）x²-2x-3="0" （用适当的方法）

阅读下面的材料：
小明在学习中遇到这样一个问题：若1≤x≤m，求二次函数的最大值．他画图研究后发现，和时的函数值相等，于是他认为需要对进行分类讨论．他的解答过程如下：

∵二次函数的对称轴为直线，
∴由对称性可知，和时的函数值相等．
∴若1≤m＜5，则时，的最大值为2；
若m≥5，则时，的最大值为．
请你参考小明的思路，解答下列问题：
（1）当≤x≤4时，二次函数的最大值为_______；
（2）若p≤x≤2，求二次函数的最大值；
（3）若t≤x≤t+2时，二次函数的最大值为31，则的值为_______．

图中是抛物线形拱桥，当水面宽为4米时，拱顶距离水面2米；当水面高度下降1米时，水面宽度为多少米？

把下列各数填在相应的大括号内，, , , , , ,  -
（1）整数集合：｛…｝
（2）分数集合：｛…｝
（3）非负数集合：｛…｝

（本题4分）计算：.

如图，已知图（1）和图（2）中的每个小正方形的边长都是1个单位．
（1）将图（1）中的格点△ABC，先向右平移3个单位，再向上平移2个单位，得到△A₁B₁C₁，请你在图（1）中画出△A₁B₁C₁；
（2）在图（2）中画出一个与格点△DEF相似，但相似比不等于1的格点三角形．

如图，四边形ABCD与四边形A′B′C′D′相似，AB＝18，A′B′＝6，B′C′＝8，C′D′＝7．求∠A、∠D、BC、CD．

如图，AB为⊙O的直径，直线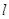与⊙O相切于点C，过点A作AD⊥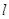于点D，交⊙O于点E．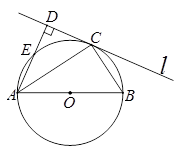

（1）求证：∠CAD＝∠BAC；[（2）若sin∠BAC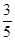＝，BC＝6，求DE的长．