初中数学解答题

如图①，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在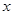轴的正半轴上，点C在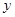轴的正半轴上，OA=5，OC=4.
（1）在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标；
（2）如图②，若AE上有一动点P（不与A、E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为秒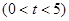，过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式；当取何值时，S有最大值？最大值是多少？
（3）在（2）的条件下，当为何值时，以A、M、E为顶点的三角形为等腰三角形，并求出相应时刻点M的坐标.

如图, 已知直线分别与轴, 轴交于两点, 点在轴上. 以点为圆心的⊙与直线相切于点, 连接.

(1) 求证: ∽;
（2）如果⊙的半径为, 求出点的坐标, 并写出以为顶点, 且过点的抛物线的解析式;
(3) 在(2)的条件下, 在此抛物线上是否存在点, 使得以三点为顶点的三角形与相似? 如果存在, 请求出所有符合条件的点的坐标; 如果不存在, 请说明理由.

在平面直角坐标系xOy中，抛物线y= -x²+x+m²-3m+2 与x轴的交点分别为原点O和点A，点B(2，n)在这条抛物线上。

(1) 求点B的坐标；
(2) 点P在线段OA上，从O点出发向A点运动，过P点作x轴的垂线，与直线OB交于点E。延长PE到点D。使得ED=PE。 以PD为斜边在PD右侧作等腰直角三角形PCD(当P点运动时，C点、D点也随之运动)
j当等腰直角三角形PCD的顶点C落在此抛物线上时，求OP的长；
k若P点从O点出发向A点作匀速运动，速度为每秒1个单位，同时线段OA上另一点Q从A点出发向O点作匀速运动，速度为每秒2个单位(当Q点到达O点时停止运动，P点也同时停止运动)。过Q点作x轴的垂线，与直线AB交于点F。延长QF到点M，使得FM=QF，以QM为斜边，在QM的左侧作等腰直角三角形QMN(当Q点运动时，M点，N点也随之运动)。若P点运动到t秒时，两个等腰直角三角形分别有一条直角边恰好落在同一条直线上，求此刻t的值。

如图1，已知矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3；抛物线经过坐标原点O和x轴上另一点E（4,0）

图1图2
（1）当x取何值时，该抛物线的最大值是多少？
（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）.
① 当时，判断点P是否在直线ME上，并说明理由；
② 以P、N、C、D为顶点的多边形面积是否可能为5，若有可能，求出此时N点的坐标；若无可能，请说明理由．

已知,矩形中,,,的垂直平分线分别交、于点、,垂足为.
(1)如图1,连接、.求证四边形为菱形,并求的长；
(2)如图2,动点、分别从、两点同时出发,沿和各边匀速运动一周.即点自→→→停止,点自→→→停止.在运动过程中,已知点的速度为每秒5,点的速度为每秒4,运动时间为秒,当、、、四点为顶点的四边形是平行四边形时,求的值.

在平面直角坐标系中，抛物线y=ax²+bx+2的图象过和，与轴交于点，与轴交于另一点，点是原点关于点的对称点，连结、，设点。

（1）求抛物线的解析式；
（2）连结、，①求的值；②将绕点旋转，在旋转过程中如图（2），线段和的比值会变吗？请说明理由；
（3）设点是直线上方的抛物线上一点，连结，以为边作图示一侧的正方形，随着点的运动，正方形的大小，位置也随之改变，当顶点或恰好落在轴上时，直接写出对应点的坐标。

已知抛物线y=ax²+bx+c ，当x=0时，有最小值为1 ；且在直线y=2上截得的线段长为4 .

（1）求此抛物线的解析式；
（2）若点P是抛物线的任意一点，记点P到X轴的距离为d₁，点P 与点 F （0，2）的距离为d ₂，猜想d₁、 d ₂的大小关系，并证明；
（3）若直线PF交此抛物线于另一点Q（异于P点）。 试判断以PQ为直径的圆与x 轴的位置关系，并说明理由。

已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F　，使CF＝CE，连结DF，交BE的延长线于点G，连结OG．
⑴ 求证：△BCE≌△DCF；
⑵ OG与BF有什么数量关系？证明你的结论；
⑶ 若GE·GB＝4－2，求　正方形ABCD的面积．

已知二次函数：
(1) 证明：当m为整数时，抛物线与x轴交点的横坐标均为整数；
(2) 以抛物线的顶点A为等腰Rt△的直角顶点，作该抛物线的内接等腰Rt△ABC（B、C两点在抛物线上），求Rt△ABC的面积（图中给出的是m取某一值时的示意图）；
(3) 若抛物线与直线y＝7交点的横坐标均为整数，求整数m的值.

已知抛物线交y轴于点A，交x轴于点B,C（点B在点C的右侧）.过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P，过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
（1）写出A，B，C三点的坐标；
（2）若点P位于抛物线的对称轴的右侧：
①如果以A，P，Q三点构成的三角形与△AOC相似，求出点P的坐标；
②若将△APQ沿AP对折，点Q的对应点为点M.是否存在点P，使得点M落在x轴上.若存在，求出点P的坐标；若不存在，请说明理由.

如图，已知抛物线y=ax＋bx＋c经过A（－3，0）、B（1，0）、C（0，3）三点，求：（1）抛物线解析式
（2）若抛物线的顶点为P，求∠PAC的正切值
（3）若以点A、C、P、M为顶点的四边形是平行四边形，求点M的坐标

如图①在梯形ABCD中，AD∥BC。AB=DC
（1）如果点P，E和F分别是BC，AC和BD的中点，证明：AB=PE＋PF
（2）如果点P是线段BC上任意一点（中点除外），PE∥AB，PF∥DC，如图②所示，那么AB=PE＋PF这个结论还成立吗？请说明理由
（3）如果点P在线段BC的延长线上， PE∥AB，PF∥DC，其他条件不变，那么结论AB=PE＋PF是否成立？直接写出结论，不必证明。

为了发展旅游经济，我市某风景区对门票采用灵活的售票方法吸引游客，门票的定价为每人50元，，非节日打a折售票，节假日按团队人数分段定价售票，即m人一下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人的部分的游客打b折售票，设某旅游团人数为x人，非节假日购票款为y（元），节假日购票款为y（元）。y、y与x之间的函数图像如图所示

（1）观察图像可知a=，b=，m=
（2）直接写出y， y与x之间的函数解析式
（3）某旅行社导游王娜于5月1日带A团，5月20日（非节假日）带B团到该景区旅游，共付门票款1900元，A、B两个团队合计50人，求A、B两个团队各有多少人？

某农场去年种植了10亩地的南瓜，亩产量为2000千克，根据时常需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜的种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60000千克，求南瓜亩产量的增长率。

如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，线段CD=10，连接BD
（1）求证：∠CDE=2∠B
（2）若BD：AB=：2，求⊙O的半径及弦DF的长