如图,丹东防汛指挥部发现鸭绿江边一处长500米高10米背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固,经调查论证,防洪指挥部专家组指定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:
(1)求加固后坝底增加的宽度AF
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2,B布袋中有三个完全相同的小球,分别标有数字-1,-2和-3,小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B布袋中随机取出一个小球,记录其标有的数字为b,这样就确定一个点Q的坐标为(a,b)
(1)用列表或树状图的方法写出点Q的所有可能坐标
(2)求点Q落在直线y=x-3上的概率
近几年,丹东市加大中职教育投入力度,取得了良好的社会效果,某学校随机调查了九年级m名学生的升学意向,并根据结果绘制出如下两幅不完整的统计图,请根据图中信息解答下列问题
(1)m=
(2)扇形统计图中“职高”对应的扇形圆心角=
(3)补全条形统计图
(4)若该校九年级学生有900人,估计该校共有多少名毕业生的升学意向是职高?
|


如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.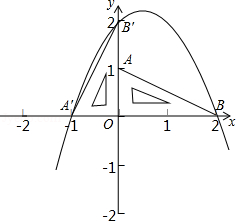
深化理解(本小题满分9分)
如图,在平面直角坐标系中,点C的坐标为(0,4),A是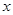 轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作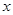 轴的垂线、过点C作
轴的垂线、过点C作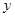 轴的垂线,两直线交于点D,直线DB交
轴的垂线,两直线交于点D,直线DB交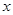 轴于一点E.
轴于一点E.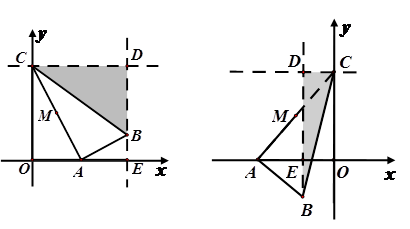
设A点的横坐标为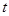 ,
,
(1)若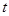 =3,则点B的坐标为▲,若
=3,则点B的坐标为▲,若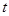 =-3,,则点B的坐标为▲;
=-3,,则点B的坐标为▲;
(2)若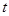 >0,△BCD的面积为
>0,△BCD的面积为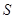 ,则
,则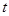 为何值时,
为何值时, ?
?
(3)是否存在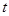 ,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时
,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时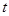 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,矩形DEFG的顶点G与△ABC的顶点C重合,边GD、GF分别与AC,BC重合。GD=12,GF=16,矩形DEFG沿射线CB的方向以每秒4个单位长的速度匀速运动,点Q从点B出发沿BA方向以每秒5个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点H,矩形DEFG、点Q同时出发,当点Q到达点A时停止运动,矩形DEFG也随之停止运动。设矩形DEFG、点Q运动的时间是t秒(t>0)。(1)求线段DF的长;
(2)求运动过程中,矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式(写出自变量的取值范围);
(3)射线QK能否把矩形DEFG分成面积相等的两部分?若能,求出t值,若不能,说明理由;
(4)连接DH,当DH∥AB时,请直接写出t值。
如图,一次函数 的图像与反比例函数
的图像与反比例函数 的图像交于
的图像交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知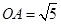 ,点
,点 的坐标为
的坐标为 ,过点
,过点 作
作 轴,垂足为
轴,垂足为 。
。
(1)求反比例函数和一次函数的解析式;
(2)求 的面积。
的面积。
(3)根据图像回答:当x 为何值时,一次函数的函数值大于
反比例函数的函数值?
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:
| 1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
(1)根据上表提供的数据填写下表:
| 优秀率 |
中位数 |
方差 |
|
| 甲班 |
|||
| 乙班 |
(2)根据以上信息,你认为应该把冠军奖状发给哪一个班级? 简述理由.
如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米 的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
如图,将一张矩形纸片 沿EF折叠,使点
沿EF折叠,使点 落在
落在 边上的点B处;沿BG折叠,使点
边上的点B处;沿BG折叠,使点 落在点D处,且BD过F点.
落在点D处,且BD过F点.试判断四边形BEFG的形状,并证明你的结论.
当∠BFE为多少度时,四边形BEFG是菱形.

某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。
⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。
⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系(不需要证明)
试题篮
()