初中数学解答题

如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标为（0，8），点C的坐标为（10，0），OB＝OC．点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H.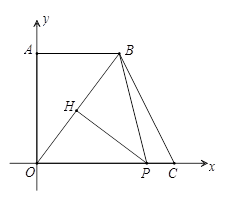

（1）求点B的坐标；
（2）设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式；当t为何值时，△HBP的面积最大，并求出最大面积；
（3）分别以P、H为圆心，PC、HB为半径作⊙P和⊙H，当两圆外切时，求此时t的值.

如图1，抛物线与轴交于两点，与轴交于点，连结AC，若

求抛物线的解析式
抛物线对称轴上有一动点P，当时，求出点的坐标；
如图2所示，连结，是线段上（不与、重合）的一个动点.过点作直线，交抛物线于点，连结、，设点的横坐标为．当t为何值时，的面积最大？最大面积为多少？

如图，在平面直角坐标系中，直线=分别与轴，轴相交于两点，点是轴的负半轴上的一个动点，以为圆心，3为半径作.
连结，若，试判断与轴的位置关系，并说明理由；
当为何值时，以与直线=的两个交点和圆心为顶点的三角形是正三角形？

使得函数值为零的自变量的值称为函数的零点．例如，对于函数，令，可得，我们就说是函数的零点．请根据零点的定义解决下列问题：已知函数（m为常数）．
当m=0时，求该函数的零点
证明：无论m取何值，该函数总有两个零点；
设函数的两个零点分别为和，且，此时函数图象与轴的交点分别为A、B（点A在点B左侧），点M在直线上，当MA+MB最小时，求直线AM的函数解析式．

甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时(从甲车出发时开始计时)．图中折线、线段分别表示甲、乙两车所行路程(千米)与时间(小时)之间的函数关系对应的图象(线段表示甲出发不足2小时因故停车检修)．请根据图象所提供的信息，解决如下问题：

(1)求乙车所行路程与时间的函数关系式；
(2)求两车在途中第二次相遇时，它们距出发地的路程；
(3)乙车出发多长时间，甲、乙两车相距80千米？(写出解题过程)

如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．
（1）求证：KE=GE；
（2）若=KD·GE，试判断AC与EF的位置关系，并说明理由；
（3） 在（2）的条件下，若sinE=，AK=，求FG的长．

如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．

（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=，CQ=时，P、Q两点间的距离 (用含的代数式表示)．

甲、乙两商场自行定价销售某一商品．
（1）甲商场将该商品提价15%后的售价为1.15元，则该商品在甲商场的原价为 ▲元；
（2）乙商场将该商品提价20%后，用6元钱购买该商品的件数比没提价前少买1件，求该商品在乙商场的原价是多少？
（3）在（1）、（2）小题的条件下，甲、乙两商场把该商品均按原价进行了两次价格调整．
甲商场：第一次提价的百分率是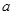，第二次提价的百分率是；
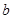乙商场：两次提价的百分率都是(．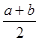
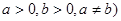请问甲、乙两商场，哪个商场的提价较多？请说明理由．

两块完全相同的三角形纸板ABC和DEF，按如图所示的方式叠放，阴影部分为重叠部分，点O为边
AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等？为什么？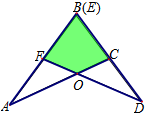

为响应环保组织提出的“低碳生活”的号召，李明决定不开汽车而改骑自行车上班．有一天，李明骑自行车从家里到工厂上班，途中因自行车发生故障，修车耽误了一段时间，车修好后继续骑行，直至到达工厂（假设在骑自行车过程中匀速行驶）．李明离家的距离y（米）与离家时间x（分钟）的关系表示如下图：

李明从家出发到出现故障时的速度为米／分钟；
李明修车用时分钟；
求线段BC所对应的函数关系式（不要求写出自变量的取值范围）．

已知关于x的一元二次方程x² = 2(1—m)x—m²的两实数根为x₁，x₂，
求m的取值范围；
设y = x₁ + x₂，当y取得最小值时，求相应m的值，并求出y的最小值。

某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元。为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施。经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。求：
（1）若商场平均每天要赢利1200元，且让顾客感到实惠，每件衬衫应降价多少元？
（2）用配方法说明，每件衬衫降价多少元时，商场平均每天赢利最多，最多是多少？

某中学八年级共有400名学生，学校为了增强学生的安全意识，在本年级进行了一次安全知识测验．为了了解这次测验的成绩状况，从中抽取了50名学生的成绩，将所得数据整理后，画出频数分布直方图如图所示．
(1)图中第五个小组的频数是；第四个小组的频率为；第五个小组的频率是；
(2)这次测验中，估计八年级全体学生中成绩在59．5～69．5中的人数约是多少?
(3)试估计这次测验中，八年级全体学生的平均成绩是多少?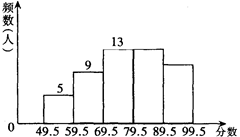

某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售。
（1）求平均每次下调的百分率。
（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元。
试问哪种方案更优惠？

如图，在直角坐标系中，⊙O的圆心O在坐标原点，直径AB=8，点P是直径AB上的一个动点（点P不与A、B两点重合），过点P的直线PQ的解析式为，当直线PQ交y轴于Q，交⊙O于C、D两点时，过点C作CE垂直于x轴交⊙O于点E，过点E作EG垂直于y轴，垂足为G，过点C作CF垂直于y轴，垂足为F，连接DE．

（1）点P在运动过程中，∠CPB=；
（2）当m=3时，试求矩形CEGF的面积；
（3）当P在运动过程中，探索的值是否会发生变化？如果发生变化，请你说明理由；如果不发生变化，请你求出这个不变的值；
（4）如果点P在射线AB上运动，当△PDE的面积为4时，请你求出CD的长度