已知二次函数 (m为常数).
(m为常数).求证:不论m为何值,该二次函数图象的顶点P都在函数
 的图象上;
的图象上;若顶点P的横、纵坐标相等,求P点坐标
有3张背面相同的卡片,正面分别写着数字“1”、“2”、“3”.将卡片洗匀后背面朝上放在桌面上.若小明从中任意抽取一张,则抽到奇数的概率是 ;
若小明从中任意抽取一张后,小亮再从剩余的两张卡片中抽取一张,规定:抽到的两张卡片上的数字之和为奇数,则小明胜,否则小亮胜.你认为这个游戏公平吗?请用 画树状图或列表的方法说明你的理由.
为了了解某校九年级学生的体质健康状况,从该校九年级学生中随机抽取了40名学生进行调查.将调查结果绘制成如下统计表和统计图.请根据所给信息解答下列问题:]
| 成绩 |
频数 |
频率 |
| 不及格 |
3 |
0.075 |
| 及格 |
|
0.2 |
| 良好 |
17 |
0.425 |
| 优秀 |
|
|
| 合计 |
40 |
1 |

补充完成频数统计表;
求出扇形统计图的“优秀”部分的圆心角度数;
若该校九年级共有200名学生,试估计该校体质健康状况达到良好及以上的学生总人数.
如图①,在平面直角坐标系中,等腰直角△AOB的斜边OB在x轴上,顶点A的坐标为(3,3),AD为斜边上的高.抛物线y=ax2+2x与直线y=x交于点O、C,点C的横坐标为6.点P在x轴的正半轴上,过点P作PE∥y轴,交射线OA于点E.设点P的横坐标为m,以A、B、D、E为顶点的四边形的面积为S.求OA所在直线的解析式
求a的值
当m≠3时,求S与m的函数关系式.
如图②,设直线PE交射线OC于点R,交抛物线于点Q.以RQ为一边,在RQ的右侧作矩形RQMN,其中RN=.直接写出矩形RQMN与△AOB重叠部分为轴对称图形时m的取值范围.

如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥ 轴于点C,A
轴于点C,A ,B
,B .动点P从O点出发,沿
.动点P从O点出发,沿 轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设
轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设 点移动的时间为秒,△OPQ与直角梯形OABC重叠部分的面积为S.
点移动的时间为秒,△OPQ与直角梯形OABC重叠部分的面积为S.
求经过O、A、B三点的抛物线解析式;
求S与t的函数关系式;
将△OPQ绕着点
 逆时针旋转90°,是否存在t,使得△OPQ的顶点为O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
逆时针旋转90°,是否存在t,使得△OPQ的顶点为O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
在平面直角坐标系xOy中,抛物线 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.求此抛物线的解析式
点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.
如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO= (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
如图,将一把直角三角板的直角顶点放置于原点O,两直角边与抛物线 交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:
交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:当m=1时,n=__ ▲; 当m=2时,n=__ ▲试猜想m与n满足的关系,并证明你猜想的结论。
连接M、N,若△OMN的面积为S,求S关于m的函数关系式。
当三角板绕点O旋转到某一位置时,恰好使得∠MNO=30°,此时过M作MA⊥x轴,垂足为A,求出△OMA的面积
当m=2时,抛物线上是否存在一点P使M、N、O、P四点构成梯形,若存在,直接写出所有满足条件的点P的坐标;若不存在,说明理由。

如图,在梯形ABCD中,AD∥BC,AD=3,DC=5,AB=4 ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.求BC的长
当MN∥AB时,求t的值
试探究:t为何值时,△MNC为等腰三角形.

在平面直角坐标系中,已知抛物线 与
与 轴交于点
轴交于点 (-1,0)、
(-1,0)、 (3,0),与
(3,0),与 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为 .
.
求抛物线解析式及顶点
 的坐标;
的坐标;如图,过点E作BC平行线,交
 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有:.
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有:.将抛物线向下平移,与
 轴交于点M、N,与
轴交于点M、N,与 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
已知:如图,在平面直角坐标系中,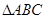 是直角三角形,
是直角三角形,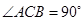 ,点
,点 的坐标分别为
的坐标分别为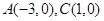 ,
,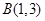
求过点
 的直线的函数表达式
的直线的函数表达式在
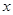 轴上找一点
轴上找一点 ,连接
,连接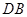 ,使得
,使得 与
与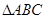 相似(不包括全等),并求点
相似(不包括全等),并求点 的坐标;
的坐标;在⑵的条件下,如
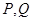 分别是
分别是 和
和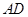 上的动点,连接
上的动点,连接 ,设
,设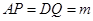 ,问是否存在这样的
,问是否存在这样的 使得
使得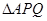 与
与 相似,如果存在,请求出
相似,如果存在,请求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
如图,已知正方形ABCD,点P为射线BA上的一点(不和点A,B重合),过P作PE⊥CP,且CP=PE.过E作EF∥CD交射线BD于F.若CB=6,PB=2,则EF=;DF=;

请探究BF,DG和CD这三条线段之间的数量关系,写出你的结论并证明;
如图2,点P在线段BA的延长线上,当tan∠BPC=时,四边形EFCD与四边形PEFC的面积之比为
 .
.
在一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.第一小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图1);再沿GC折叠,使点B落在EF上的点B'处(如图2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.

第二小组的同学,在一个矩形纸片上按照图3的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图4.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.

探究活动结束后,老师给大家留下了一道探究题:如图5,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.

已知:在△ABC中,AB=AC,∠B=30°,BC=6,动点P以每秒 个单位从点B出发沿线段BA、AC运动,过点P作边长为3的等边△FDE,使得点D在线段BC上,点E在线段DC上.
个单位从点B出发沿线段BA、AC运动,过点P作边长为3的等边△FDE,使得点D在线段BC上,点E在线段DC上.如图(1),当EF经过点A时,动点P运动时间t为多少?
设点P运动t秒时,△ABC与△DEF重叠部分面积为S,求S关于t的函数关系式
如图(2),在点P的运动过程中,是否存在时间t,使得以点P为圆心,AP为半径的圆与△FDE三边所在的直线相切.如果存在,请直接写出t的值;如不存在,说明理由.


试题篮
()