解决问题:如图,已知正方形ABCD,点E是边AB上一动点,点F在AB边或其延长线上,点G在边AD上.连结ED,FG,交点为H.如图1,若AE=BF=GD,请直接写出∠EHF=▲°;
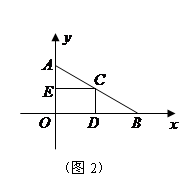
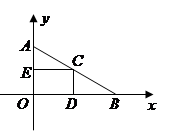
如图2,若EF =
 CD,GD=
CD,GD= AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出tanα.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出tanα.

如图1,点C、B分别为抛物线C1:y1=x2+1,抛物线C2:y2=a2x2+b2x+c2的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB=BD.求点A的坐标:
如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”.其他条件不变,求CD的长和a2的值;
如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 2
 (直接写结果).
(直接写结果).
如图,已知抛物线y=x -ax+a
-ax+a -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
求抛物线的解析式
若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标
P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
如图1,在平面直角坐标系中,已知点 ,点
,点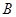 在
在 正半轴上,且
正半轴上,且 .动点
.动点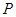 在线段
在线段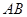 上从点
上从点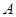 向点
向点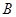 以每秒
以每秒 个单位的速度运动,设运动时间为秒.点M、N在
个单位的速度运动,设运动时间为秒.点M、N在 轴上,且
轴上,且 是等边三角形.
是等边三角形.求点B的坐标
求等边
 的边长(用的代数式表示),并求出当等边
的边长(用的代数式表示),并求出当等边 的顶点
的顶点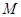 运动到与原点
运动到与原点 重合时的值;
重合时的值;如果取
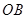 的中点
的中点 ,以
,以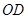 为边在
为边在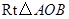 内部作如图2所示的矩形
内部作如图2所示的矩形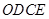 ,点
,点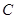 在线段
在线段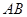 上.设等边
上.设等边 和矩形
和矩形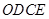 重叠部分的面积为
重叠部分的面积为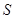 ,请求出当
,请求出当 秒时,
秒时,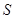 与的函数关系式,并求出
与的函数关系式,并求出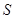 的最大值.
的最大值.

如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.试猜想线段BG和AE的数量关系,请直接写出你得到的结论.
将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值.


如图,矩形ABCD中,AB=3,BC=4,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积, 表示矩形NFQC的面积
表示矩形NFQC的面积
(1)S与 吗?请说明理由.
吗?请说明理由.
(2)设AE=x,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
(3)如图2,连结BE,当AE为何值时, 是等腰三角形.
是等腰三角形.
如图,已知直线 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
(1)求证:
 ∽
∽ ;
;
(2)如果圆M的半径为 ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;
(3)在(2)的条件下,试问此抛物线上是否存在点P,使得以P、A、M三点为顶点的三角形与 相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C两点重合),线段BE的垂直平分线交射线AC于点P,联结DP,PE.
(1)若四边形ABCD是正方形,猜想PD与PE的关系,并证明你的结论.
(2)若四边形ABCD是矩形,(1)中的PD与PE的关系还成立吗?(填:成立或不成立).
(3)若四边形ABCD是矩形,AB=6,cos∠ACD= ,设AP=x,△PCE的面积为y,当AP>
,设AP=x,△PCE的面积为y,当AP> AC时,求y与x之间的函数关系式.
AC时,求y与x之间的函数关系式.
已知:如图,二次函数y=a(x+1)2-4的图象与x轴分别交于A、B两点,与y轴交于点D,点C是二次函数y=a(x+1)2-4的图象的顶点,CD= .
.
(1)求a的值.
(2)点M在二次函数y=a(x+1)2-4图象的对称轴上,
且∠AMC=∠BDO,求点M的坐标.
(3)将二次函数y=a(x+1)2-4的图象向下平移k(k>0)个单位,平移后的图象与直线CD分别交于E、F两点(点F在点E左侧),设平移后的二次函数的图象的顶点为C1,与y轴的交点为D1,是否存在实数k,使得CF⊥FC1,若存在,求出k的值;若不存在,请说明理由.
已知二次函数
(1)求证:无论a为任何实数,二次函数的图象与x轴
总有两个交点.
(2)当x≥2时,函数值 随
随 的增大而减小,求
的增大而减小,求 的取
的取
值范围.
(3)以二次函数 图象的顶点
图象的顶点 为一个顶点作该二次函数图象的内接正三角形
为一个顶点作该二次函数图象的内接正三角形 (M,N两点在二次函数的图象上),请问:△
(M,N两点在二次函数的图象上),请问:△ 的面积是与a无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
的面积是与a无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
如图,在△ABC中,AB=AC,以AB边的中点O为圆心,线段OA的长为半径作圆,分别交BC、AC边于点D、E,DF⊥AC于点F,延长FD交AB延长线于点G .
(1)求证:FD是⊙O的切线.
(2)若BC=AD=4,求 的值.
的值.
 中,
中, ,
, ,
, cm.长为1cm的线段
cm.长为1cm的线段 在
在 的边
的边 上沿
上沿 方向以1cm/s的速度向点
方向以1cm/s的速度向点 运动(运动前点
运动(运动前点 与点
与点 重合).过
重合).过 分别作
分别作 的垂线交直角边于
的垂线交直角边于 两点,线段
两点,线段 运动的时间为s.
运动的时间为s.
(1)若 的面积为
的面积为 ,写出
,写出 与的函数关系式(写出自变量的取值范围);
与的函数关系式(写出自变量的取值范围);
(2)线段 运动过程中,四边形
运动过程中,四边形 有可能成为矩形吗?若有可能,求出此时的值;若不可能,说明理由;
有可能成为矩形吗?若有可能,求出此时的值;若不可能,说明理由;
(3)为何值时,以 为顶点的三角形与
为顶点的三角形与 相似?
相似?
如图,抛物线 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
(1)求a,b的值;
(2)将45°角的顶点P在线段OB上滑动(不与点B重合),该角的一边过点D,另一边与BD交于点Q,设P(x,0),y2= DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式;
(3)在同一平面直角坐标系中,两条直线x = m,x = m+ 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为 ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由.
实践与探究:
对于任意正实数a、b,∵ ≥0, ∴
≥0, ∴ ≥0,∴
≥0,∴ ≥
≥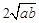
只有当a=b时,等号成立。
结论:在 ≥
≥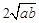 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 。根据上述内容,回答下列问题:
。根据上述内容,回答下列问题:
(1)若m>0,只有当m=时,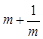 有最小值;
有最小值;
若m>0,只有当m=时,2 有最小值.
有最小值.
(2)如图,已知直线L1: 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.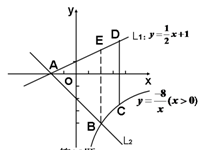
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1
于点D,试求当线段CD最短时,点A、B、C、D围成的四边形面积.
试题篮
()