如图,在平面直角坐标系中,O为坐标原点,已知A(2, ),C(4,0),E点从O出发,以每秒1个单位的速度,沿边OC向C点运动,P点从O点出发,以每秒2个单位的速度,沿边OA与边AC向C运动,E、P两点同时出发,设运动时间为t秒。
),C(4,0),E点从O出发,以每秒1个单位的速度,沿边OC向C点运动,P点从O点出发,以每秒2个单位的速度,沿边OA与边AC向C运动,E、P两点同时出发,设运动时间为t秒。
(1)求∠AOC的度数,
(2)过 E作EH⊥AC于H,当t为何值时,△EPH是等边三角形。
(3)设四边形OEHP的面积S,求S关于t的函数表达式,并求出其最大值。
(4)当△OPE与以E、H、P为顶点的三角形相似,求P点坐标。
如图,在Rt△ABC中,∠C=90°,AC=4㎝,BC=5㎝,D是BC边上一点,CD=3㎝,点P为边AC上一动点(点P与A、C不重合),过点P作PE// BC,交AD于点E.点P以1㎝/s的速度从A到C匀速运动。设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出
 的取值范围;
的取值范围;当t为何值时,以PE为半径的⊙E与以DB为半径的⊙D外切?并求此时∠DPE的正切值;
将△ABD沿直线AD翻折,得到△AB’D,连接B’ C.如果∠ACE=∠BCB’,求t的值.

在图形的全等变换中,有旋转变换,翻折(轴对称)变换和平移变换.一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
(1)第一小组的同学发现,在如图1-1的矩形ABCD中,AC、BD相交于点O,Rt△ADC可以由Rt△ABC经过一种变换得到,请你写出这种变换的过程▲.
(2)第二小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图2-1);再沿GC折叠,使点B落在EF上的点B'处(如图2-2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.
(3)第三小组的同学,在一个矩形纸片上按照图3-1的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图3-2.已知AH=AI,判断以AD、AF和AH为三边能否构成三角形?若能构成,请判断这个三角形的形状,若不能构成,请说明理由.
(4)探究活动结束后,老师给大家留下了一道探究题:如图4-1,已知AA'=BB'=CC'=4,∠AOB'=∠BOC'=∠COA'=60°,请利用图形变换探究S△AOB'+S△BOC'+S△COA'与 的大小关系.
的大小关系.
如图,在平面直角坐标系xoy中,抛物线y= x2-
x2- x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,C两点的坐标和抛物线的顶点M坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<4.5时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.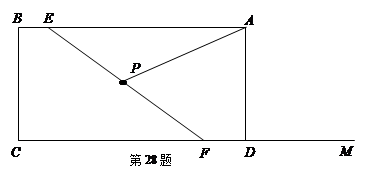
在点E运动过程中,AP的长度是如何变化的?( )
| A.一直变短 | B.一直变长 | C.先变长后变短 | D.先变短后变长 |
在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在.
以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
一位数学老师参加本市自来水价格听证会后,编写了一道应用题,题目如下:节约用水、保护水资源,是科学发展观的重要体现.依据这种理念,本市制定了一套节约用水的管理措施,其中规定每月用水量超过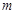 (吨)时,超过部分每吨加收环境保护费
(吨)时,超过部分每吨加收环境保护费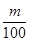 元.下图反映了每月收取的水费
元.下图反映了每月收取的水费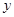 (元)与每月用水量
(元)与每月用水量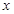 (吨)之间的函数关系.
(吨)之间的函数关系.
请你解答下列问题:将m看作已知量,分别写出当0<x<m和x>m时,
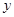 与
与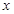 之间的函数关系式;
之间的函数关系式;按上述方案,一家酒店四、五两月用水量及缴费情况如下表所示,那么,这家酒店四、五两月的水费分别是按哪种方案计算的?并求出
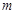 的值.
的值.
| 月份 |
用水量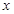 (吨) (吨) |
水费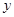 (元) (元) |
| 四月 |
35 |
59.5 |
| 五月 |
80 |
151 |
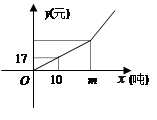
七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
|
|





如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.
判断直线BD与⊙O的位置关系,并说明理由;
连接CD,若CD=5,求AB的长.
如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长.(参考数据:=1.73)
图①表示的是某综合商场今年1—5月的商品各月销售总额的情况,图②表示商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
来自商场财务部的数据报告表明,商场1—5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
商场服装部5月份的销售额是多少万元?
小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了,你同意他的看法吗?请说明理由.
在四边形 中,对角线AC与BD交于点O,△ABO≌△CDO.
中,对角线AC与BD交于点O,△ABO≌△CDO.求证:四边形
 为平行四边形;
为平行四边形;若∠ABO=∠DCO,求证:四边形
 为矩形.
为矩形.
问题背景:
如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
探究发现:如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,则此时铁片的形状是 _______,给出证明,并通过计算说明此时铁片都能穿过圆孔;

拓展迁移:如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片;

①当BE=DF= 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围 .
某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
| 项目 |
第一年的工资(万元) |
一年后的计算方法 |
| 基础工资 |
1 |
每年的增长率相同 |
| 住房补贴 |
0.04 |
每年增加0.04 |
| 医疗费 |
0.1384 |
固定不变 |
设基础工资每年的增长率为
 ,用含
,用含 的代数式表示第三年的基础工资为万元.
的代数式表示第三年的基础工资为万元.某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18%,问基础工资每年的增长率是多少?
某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).
请求出旗杆MN的高度.(参考数据: ≈1.4,
≈1.4, ≈1.7,结果保留整数。)
≈1.7,结果保留整数。)
试题篮
()