我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.
(1)图1中标出的是一种可能的复制结果,小明发现△A∽△B,其相似比为_________.在图1的基础上继续复制下去得到△C,若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C中含有______个小三角形;
(2)若△A是正三角形,你认为通过复制能形成的正多边形是________;
(3)请你用两

 次旋转和一次平移复制形成一个四
次旋转和一次平移复制形成一个四 边形,在图2的方框内画出草图,并仿照图1作出标记.
边形,在图2的方框内画出草图,并仿照图1作出标记.
如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为ycm.(1)当x= ▲s时,DE⊥AB;
(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;
(3)当△BEF为等腰三角形时,求x的值.

如图,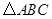 为直角三角形,
为直角三角形,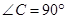 ,
,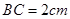 ,
,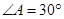 ;四边形
;四边形 为矩形,
为矩形, ,
,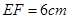 ,且点
,且点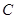 、
、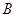 、
、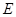 、
、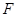 在同一条直线上,点
在同一条直线上,点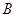 与点
与点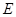 重合.
重合.
(1)求边
 的长;
的长;(2)将
 以每秒
以每秒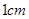 的速度沿矩形
的速度沿矩形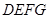 的边
的边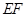 向右平移,当点
向右平移,当点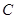 与点
与点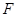 重合时停止移动,设
重合时停止移动,设 与矩形
与矩形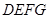 重叠部分的面积为
重叠部分的面积为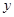 ,请求出重叠部分的面积
,请求出重叠部分的面积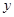 (
(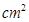 )与移动时间
)与移动时间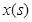 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);(3)在(2)的基础上,当
 移动至重叠部分的面积为
移动至重叠部分的面积为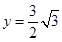
 时,将
时,将 沿边
沿边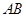 向上翻折,得到
向上翻折,得到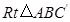 ,请求出
,请求出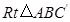 与矩形
与矩形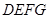 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°。(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点
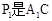 与AB的交点,点Q是
与AB的交点,点Q是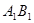 与BC的交点,求证:
与BC的交点,求证: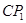 =
=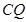 ;
;(2)在图2中,若AP1=
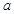 ,则CQ等于多少?
,则CQ等于多少?(3)将图2中△
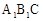 绕点C顺时针旋转到△
绕点C顺时针旋转到△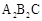 (如图3),点
(如图3),点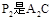 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段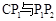 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.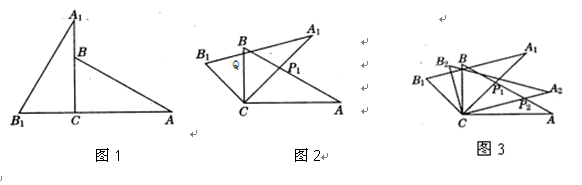
如图,在平面直角坐标系中,直线 分别交
分别交 轴,
轴, 轴于
轴于 两点,以
两点,以 为边作矩形
为边作矩形 ,
, 为
为 的中点.以
的中点.以 ,
, 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形 ,点
,点 在第一象限,设矩形
在第一象限,设矩形 与
与 重叠部分的面积为
重叠部分的面积为 .
.
(1)求点
 的坐标;
的坐标;(2)当
 值由小到大变化时,求
值由小到大变化时,求 与
与 的函数关系式;
的函数关系式;(3)若在直线
 上存在点
上存在点 ,使
,使 等于
等于 ,请直接写出
,请直接写出 的取值范围;
的取值范围;(4)在
 值的变化过程中,若
值的变化过程中,若 为等腰三角形,且
为等腰三角形,且
PC=PD,请直接写出 的值.
的值.
已知:如图①,正方形ABCD中,E为对角线BD上一点,
过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)

(本题满分12分)
已知:⊙O的直径AB=8,⊙B与⊙O相交于点C、D,⊙O的直径CF与⊙B相交于点E,设⊙B的半径为 ,OE的长为
,OE的长为 。
。
(1)如图,当点E在线段OC上时,求
 关于
关于 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;(2)当点E在直径CF上时,如果OE的长为3,求公共弦CD的长;
(3)设⊙B与AB相交于G,试问△OEG能否为等腰三角形?如果能够,请直接写出BC弧的长度(不必写过程);如果不能,请简要说明理由
(本题满分11分)
如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2分)
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3分)
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.(4分)

(一位同学拿了两块 三角尺
三角尺 ,
, 做了一个探究活动:将
做了一个探究活动:将 的直角顶点
的直角顶点 放在
放在 的斜边
的斜边 的中点处,设
的中点处,设 .
.
(1)如图(1),两三角尺的重
 叠部分为
叠部分为 ,则重叠部分的面积为,周长为.
,则重叠部分的面积为,周长为.(2)将图(1)中的
 绕顶点
绕顶点 逆时针旋转
逆时针旋转 ,得到图26(2),此时重叠部分的面积为,周长为.
,得到图26(2),此时重叠部分的面积为,周长为.(3)如果将
 绕
绕 旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为.
旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为.(4)在图(3)情况下,若
 ,求出重叠部分图形的周长.
,求出重叠部分图形的周长.
如图,Rt△ABO的顶点A是双曲线 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO=

求这两个函数的解析式
求直线与双曲线的两个交点A,C的坐标和△AOC的面积。
(本小题满分12分)已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
(1)填空:菱形ABCD的边长是▲ 、面积是
▲ 、高BE的长是▲ ;(2)探究下列问题:
①若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,在运动过程中,任何时刻都有相应的k值,使得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t =" 4" 秒时的情形,并求出k的值.
(本小题满分10分)已知:如图,⊙ 与
与 轴交于C、D两点,圆心
轴交于C、D两点,圆心 的坐标
的坐标
为(1,0),⊙ 的半径为
的半径为 ,过点C作⊙
,过点C作⊙ 的切线交
的切线交 轴于点B(-4,0)
轴于点B(-4,0)
 |
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙
 上一点,过点P作⊙A的切线与直线BC相交于点G,
上一点,过点P作⊙A的切线与直线BC相交于点G,
且∠CGP=120°,求点 的坐标;
的坐标;(3)向左移动⊙
 (圆心
(圆心 始终保持在
始终保持在 轴上),与直线BC交于E、F,在移动过程中是否存在点
轴上),与直线BC交于E、F,在移动过程中是否存在点 ,使得△AEF是直角三角形?若存在,求出点
,使得△AEF是直角三角形?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
如图,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB 以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0)。
以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0)。(1)(2分) 当t = 2时,AP =,点Q到AC的距离是;
(2)(2+2分)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;并求出S的最大值。
(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C时,请求出t的值.

(本小题满分8分)要在宽为28m的南滨路的路边安装路灯。路灯的灯臂长AC为3m,且与灯柱AB成120°的夹角(如图所示),路灯采用圆锥形灯罩,灯罩的轴线CD与灯臂AC垂直。当灯罩的轴线通过公路路面的中线时,照明效果最理想。问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m, )
)
试题篮
()