初中数学解答题

如图，在中，，将绕点按逆时针方向旋转至，点的坐标为．（1）求点的坐标；
（2）求过，三点的抛物线的解析式；

某摩托车厂本周内计划每日生产300辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）

星期	一	二	三	四	五	六	日
增减	－5	+7	－3	+4	+10	－9	－25

(1)本周三生产了多少辆摩托车？
(2)本周总生产量与计划生产量相比，是增加还是减少？
(3)产量最多的一天比产量最少的一天多生产了多少辆？

（本小题满分１２分）如图， 内接于，的平分线与交于点，与交于点，延长，与的延长线交于点，连接是的中点，连结．

（1）判断与的位置关系，写出你的结论并证明；
（2）求证：；
（3）若，求的面积．

（本小题满分8分）如图，一次函数的图象与反比例函数的图象交于两点，与轴交于点，与轴交于点，已知，，点的坐标为．
（1）求反比例函数的解析式．
（2）求一次函数的解析式．
（3）在轴上存在一点，使得与相似，请你求出点的坐标．

（本小题满分8分）
如图，从热气球上测得两建筑物、底部的俯角分别为30°和．如果这时气球的高度为90米．且点、、在同一直线上，求建筑物、间的距离．

(10分)恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地．上市时，外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中．据预测，香菇的市场价格每天每千克将上涨0.5元，但冷库存放这批香菇时每天需要支出各种费用合计340元，而且香菇在冷库中最多保存110天，同时，平均每天有6千克的香菇损坏不能出售．
（1）若存放天后，将这批香菇一次性出售，设这批香菇的销售总金额为元，试写出与之间的函数关系式．
（2）李经理想获得利润22500元，需将这批香菇存放多少天后出售？（利润＝销售总金额－收购成本－各种费用）
（3）李经理将这批香菇存放多少天后出售可获得最大利润？最大利润是多少？

（本小题满分9分）
已知关于的方程有两个不相等的实数根、，问是否存在实数，使方程的两实数根互为相反数？如果存在，求出的值；如果不存在，请说明理由。

（本小题满分7分）
如图，不透明圆锥体DEC放在水平面上，在A处灯光照射下形成影子。设BP过底面的圆心O，已知圆锥的高为m，底面半径为2m，BE=4m。求：

(1) 求∠B的度数．
　 (2)若∠ACP=2∠B，求光源A距水平面的高度。（结果保留根号）

（本题9分）
已知△ABC的两边AB、AC的长是关于x的一元二次方程x²－（2k＋3）x＋k²＋3k＋2＝0的两个实数根，第三边BC的长为5，试问：k取何值时，△ABC是以BC为斜边的直角三角形？

(本题满分8分)通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图①在△ABC中，AB＝AC，顶角A的正对记作sad A，这时sad A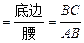．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
（1）sad 60°＝           ．
（2）对于0°＜A＜180°，∠A的正对值sad A的取值范围是
（3）如图②，在Rt△ABC中，∠C＝90°，sin A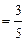，试求sad A的值

 A

 

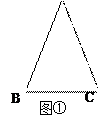如图10，为了测量一棵树AB的高度，测量者在D点立一高CD等于2m的标杆，现测量者从E处可以看到标杆顶点C与树顶A在同一条直线上，如果测得BD=20m，FD=4m，EF=1.8m，求树高。

 

如图，第一象限内半径为2的⊙C与y轴相切于点A，作直径AD，过点D作⊙C的切线l交x轴子点B，P为直线l上一动点，已知直线PA的解析式为：y＝kx＋3。
(1)设点P的纵坐标为p，写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M，与AB交于点N，则不论动点P处于直线l上（除点B以外）的什么位置时，都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明；
(3)是否存在使△AMN的面积等于的k值？若存在，请求出符合的k值；若不存在，请说明理由。

如图，在直角坐标系xOy中，点A在x轴的正半轴上，点B在y轴的正半轴上, 以OB为直径的⊙C与AB交于点D， DE与⊙C相切交x轴于点E, 且OA=cm，∠OAB="30°."

（1）求点B的坐标及直线AB的解析式;
（2）过点B作BG^EC于 F, 交x轴于点G, 求BD的长及点F的坐标;
（3）设点P从点A开始沿ABG的方向以4cm/s的速度匀速向点G移动，点Q同时
从点A开始沿AG匀速向点G移动, 当四边形CBPQ为平行四边形时, 求点Q的移动
速度.

已知：如图①，四边形是正方形，是等边三角形，为对角线（不含点）上任意一点，将绕点逆时针旋转得到，连接、、。

（I）求证：
（II）①当点在何处时，的值最小；
②当点在何处时，的值最小，并说明理由；

（III）当的最小值为时，求正方形的边长。

如图，在平面直角坐标系中，抛物线向左平移1个单位，再向下平移4个单位，得到抛物线.所得抛物线与轴交于两点（点在点的左边），与轴交于点，顶点为.
（1）求的值；
（2）求直线AC的函数解析式。
（3）在线段上是否存在点，使与相似.若存在，求出点的坐标；若不存在，说明理由.