初中数学解答题

(本小题满分12分)
如图，在平面直角坐标系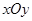中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知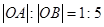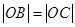，，△ABC的面积，抛物线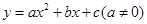
经过A、B、C三点。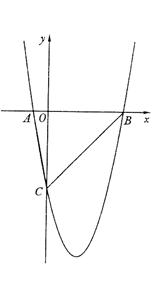

(1)求此抛物线的函数表达式；
(2)设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；
(3)在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为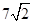？若存在，求出点M的坐标；若不存在，请说明理由．

(本小题满分1 0分)
如图，已知线段AB∥CD，AD与B C相交于点K，E是线段AD上一动点。

(1)若BK=KC，求的值；
(2)连接BE，若BE平分∠ABC，则当AE= AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明．再探究：当AE=AD (n>2)，而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论，不必证明．

已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.

(1)填空：菱形ABCD的边长是▲、面积是▲、高BE的长是▲；
(2)探究下列问题：
若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时
②△APQ的面积S关于t的函数关系式，以及S的最大值；
（3）在运动过程中是否存在某一时刻使得△APQ为等腰三角形，若存在求出t的值；若不存在说明理由.

（本题10分）如右图，点A是△ABC和△ADE的公共顶点，∠BAC＋∠DAE＝180°，AB＝AE，AC＝AD，点M是DE的中点，直线AM交直线BC于点N．将△ADE绕点A旋转，在旋转的过程中，请探究∠ANB与∠BAE的数量关系，并加以证明.

（本题8分）把两个直角边长均为6的等腰直角三角板ABC和EFG叠放在一起（如图①），使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转（旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分（如图②）.

(1) 探究：在上述旋转过程中，BH与CK的数量关系以及四边形CHGK的面积的变化情况（直接写出探究的结果，不必写探究及推理过程）；
　　(2) 利用（1）中你得到的结论，解决下面问题：连接HK，在上述旋转过程中，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在，求出此时BH的长度；若不存在，说明理由.

把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点顺时针旋转角， 旋转后的矩形记为矩形．在旋转过程中，
（1）如图①，当点E在射线CB上时，E点坐标为；
（2）当是等边三角形时，旋转角的度数是（为锐角时）；
（3）如图②，设EF与BC交于点G，当EG=CG时，求点G的坐标．
(4) 如图③，当旋转角时，请判断矩形的对称中心H是否在以C为顶点，且经过点A的抛物线上．

如图，Rt△ABC中，∠C＝90°，BC＝6，AC＝8．点P，Q都是斜边AB上的动点，点P从B向A运动（不与点B重合），点Q从A向B运动，BP＝AQ．点D，E分别是点A，B以Q，P为对称中心的对称点，HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P、Q同时停止运动．设BP的长为x，△HDE的面积为y．

(1)求证：△DHQ∽△ABC；
(2)求y关于x的函数解析式并求y的最大值；
(3)当x为何值时，△HDE为等腰三角形？

（本题10分）已知：直角梯形OABC中，BC//OA，∠AOC＝90°，以AB为直径的OM交OC于点D、E，连结AD、BD．现以O为坐标原点，OA、OC所在直线为x轴、y轴建立如图所示直角坐标系，若抛物线y＝ax²－2ax－3a(a<0)经过点A、B、D，且B为抛物线的顶点．

(1)写出顶点B的坐标▲（用a的代数式表示）；
(2)求抛物线的解析式：
(3)在x轴下方的抛物线上是否存在这样的点P：过点P作PN⊥x轴于N，使得△PAN与△OAD相似？若存在，求出点P的坐标：若不存在，说明理由．

已知是的一个内角,抛物线的顶点在轴上.
(1)求的度数;
(2) 若求:AB边的长.

如图，在半径为r的半圆⊙O中，半径OA⊥直径BC，点E、F分别在弦AB、AC上滑动并保持AE＝CF，但点F不与A、C重合，点E不与A、B重合.

（1）求证 S_{四边形AEOF}＝；
（2）设AE＝x，S_△OEF＝y,写出y与x之间的函数关系式及自变量x的范围；
（3）当S_△OEF =S_△ABC时，求点E、F分别在AB、AC上的位置及EF的长。

(7分)某市“全国文明村”白村果农王保收获枇杷20吨，桃子12吨．现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售，已知一辆甲种货车可装枇杷4吨和桃子1吨，一辆乙种货车可装枇杷和桃子各2吨．
（1）王保如何安排甲、乙两种货车可一次性地运到销售地？有几种方案？
（2）若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王保应选择哪种方案，使运输费最少？最少运费是多少？

已知：如图1，平面直角坐标系中，四边形OABC是矩形，点A，C的坐标分别为（6，0），（0，2）．点D是线段BC上的一个动点（点D与点B，C不重合），过点D作直线＝－＋交折线O－A－B于点E．

（1）在点D运动的过程中，若△ODE的面积为S，求S与的函数关系式，并写出自变量的取值范围；
（2）如图2，当点E在线段OA上时，矩形OABC关于直线DE对称的图形为矩形O′A′B′C′，C′B′分别交CB，OA于点D，M，O′A′分别交CB，OA于点N，E．探究四边形DMEN各边之间的数量关系，并对你的结论加以证明；

（3）问题（2）中的四边形DMEN中，ME的长为____________．

已知：如图，梯形ABCD中，AD∥BC，∠B=90°，AD=，BC=，DC=，
且，点M是AB边的中点．

（1）求证：CM⊥DM；
（2）求点M到CD边的距离．（用含，的式子表示）

小明喜欢研究问题，他将一把三角板的直角顶点放在平面直角坐标系的原点处，两条直角边与抛物线交于、两点．
（1）如左图，当时，则=；

（2）对同一条抛物线，当小明将三角板绕点旋转到如右图所示的位置时，过点作轴于点，测得，求出此时点的坐标；

（3）对于同一条抛物线，当小明将三角板绕点旋转任意角度时，他惊奇地发现，若三角板的两条直角边与抛物线有交点，则线段总经过一个定点，请直接写出该定点的坐标．

如图，矩形是矩形绕点B顺时针旋转得到的．其中点在轴负半轴上，线段在轴正半轴上，点的坐标为．

(1)如果二次函数的图象经过两点且图象顶点的纵坐标为．求这个二次函数的解析式；
(2)求边所在直线的解析式；
(3)在(1)中求出的二次函数图象上是否存在点P，使得,若存在，请求出点P的坐标，若不存在，请说明理由．