已知关于 的方程 有实数根.
(1)求 的取值范围;
(2)设方程的两根分别是 、 ,且 ,试求 的值.
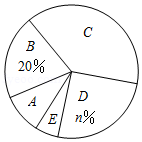
某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
| 类别 |
|
|
|
|
|
| 类型 |
新闻 |
体育 |
动画 |
娱乐 |
戏曲 |
| 人数 |
11 |
20 |
40 |
|
4 |
请你根据以上信息,回答下列问题:
(1)统计表中 的值为 ,统计图中 的值为 , 类对应扇形的圆心角为 度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
如图,矩形中,
,
,点
是对角线
的中点,过点
的直线分别交
、
边于点
、
.
(1)求证:四边形是平行四边形;
(2)当时,求
的长.

四边形 是 的圆内接四边形,线段 是 的直径,连结 、 .点 是线段 上的一点,连结 、 ,且 , , 的延长线与 的延长线相交于点 .
(1)求证:四边形 是平行四边形;
(2)若 , ,
①求证: 为等腰直角三角形;
②求 的长度.

如图所示,在平面直角坐标系 中,等腰 的边 与反比例函数 的图象相交于点 ,其中 ,点 在 轴的正半轴上,点 的坐标为 ,过点 作 轴于点 .
(1)已知一次函数的图象过点 , ,求该一次函数的表达式;
(2)若点 是线段 上的一点,满足 ,过点 作 轴于点 ,连结 ,记 的面积为 ,设 ,
①用 表示 (不需要写出 的取值范围);
②当 取最小值时,求 的值.

如图所示,已知正方形 的顶点 为正方形 对角线 、 的交点,连接 、 .
(1)求证: ;
(2)若 ,正方形 的边长为2,线段 与线段 相交于点 , ,求正方形 的边长.

某甜品店计划订购一种鲜奶,根据以往的销售经验,当天的需求量与当天的最高气温 有关,现将去年六月份(按30天计算)的有关情况统计如下:
(最高气温与需求量统计表)
| 最高气温 (单位: |
需求量(单位:杯) |
|
|
200 |
|
|
250 |
|
|
400 |
(1)求去年六月份最高气温不低于 的天数;
(2)若以最高气温位于各区间的频率估计最高气温位于该区间的概率,求去年六月份这种鲜奶一天的需求量不超过200杯的概率;
(3)若今年六月份每天的进货量均为350杯,每杯的进价为4元,售价为8元,未售出的这种鲜奶厂家以1元的价格收回销毁,假设今年与去年的情况大致一样,若今年六月份某天的最高气温 满足 (单位: ,试估计这一天销售这种鲜奶所获得的利润为多少元?

小强的爸爸准备驾车外出.启动汽车时,车载报警系统显示正前方有障碍物,此时在眼睛点 处测得汽车前端 的俯角为 ,且 ,若直线 与地面 相交于点 ,点 到地面 的垂线段 的长度为1.6米,假设眼睛 处的水平线 与地面 平行.

(1)求 的长度;
(2)假如障碍物上的点 正好位于线段 的中点位置(障碍物的横截面为长方形,且线段 为此长方形前端的边), ,若小强的爸爸将汽车沿直线 后退0.6米,通过汽车的前端 点恰好看见障碍物的顶部 点(点 为点 的对应点,点 为点 的对应点),求障碍物的高度.
已知抛物线,
为常数).
(1)若抛物线的顶点坐标为,求
,
的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求的取值范围;
(3)在(1)的条件下,存在正实数,
,当
时,恰好
,求
,
的值.
根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写"真"或"假" .
①四条边成比例的两个凸四边形相似; 命题)
②三个角分别相等的两个凸四边形相似; 命题)
③两个大小不同的正方形相似. 命题)
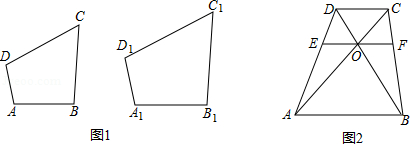
(2)如图1,在四边形 和四边形 中, , , .求证:四边形 与四边形 相似.
(3)如图2,四边形 中, , 与 相交于点 ,过点 作 分别交 , 于点 , .记四边形 的面积为 ,四边形 的面积为 ,若四边形 与四边形 相似,求 的值.
近日,长沙市教育局出台《长沙市中小学教师志愿辅导工作实施意见》,鼓励教师参与志愿辅导,某区率先示范,推出名师公益大课堂,为学生提供线上线下免费辅导,据统计,第一批公益课受益学生2万人次,第三批公益课受益学生2.42万人次.
(1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次?
试题篮
()