某种机器使用若干年后即被淘汰,该机器有一易损零件,为调查该易损零件的使用情况,随机抽取了100台已被淘汰的这种机器,经统计:每台机器在使用期内更换的该易损零件数均只有8,9,10,11这四种情况,并整理了这100台机器在使用期内更换的该易损零件数,绘制成如图所示不完整的条形统计图.
(1)请补全该条形统计图;
(2)某公司计划购买一台这种机器以及若干个该易损零件,用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率.
①求这台机器在使用期内共更换了9个该易损零件的概率;
②若在购买机器的同时购买该易损零件,则每个200元;若在使用过程中,因备用该易损零件不足,再购买,则每个500元.请你帮该公司用花在该易损零件上的费用的加权平均数进行决策:购买机器的同时应购买几个该易损零件,可使公司的花费最少?

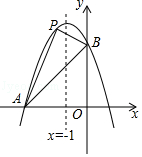
如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧上取一点D,使
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CECD,劣弧
的弧长为π,求⊙O的半径.

在一段长为1000的笔直道路AB上,甲、乙两名运动员均从A点出发进行往返跑训练.已知乙比甲先出发30秒钟,甲距A点的距离y(米)与其出发的时间x(分钟)的函数图象如图所示,乙的速度是150米/分钟,且当乙到达B点后立即按原速返回.
(1)当x为何值时,两人第一次相遇?
(2)当两人第二次相遇时,求甲的总路程.

为了测量某山(如图所示)的高度,甲在山顶A测得C处的俯角为45°,D处的俯角为30°,乙在山下测得C,D之间的距离为400米.已知B,C,D在同一水平面的同一直线上,求山高AB.(可能用到的数据:1.414,
1.732)

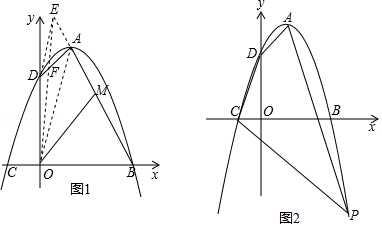
在平面直角坐标系中,顶点为
的抛物线与
轴交于
、
两点,与
轴交于点
,已知
,
.
(1)求抛物线对应的二次函数表达式;
(2)探究:如图1,连接,作
交
的延长线于点
,连接
交
于点
,
是
的中点,则
是否将四边形
分成面积相等的两部分?请说明理由;
(3)应用:如图2,是抛物线在第四象限的图象上的点,且
,连接
、
,在线段
上确定一点
,使
平分四边形
的面积,求点
的坐标.
提示:若点、
的坐标分别为
,
、
,
,则线段
的中点坐标为
,
.
为了提高农田利用效益,某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾稻”轮作模式.某农户有农田20亩,去年开始实施“虾
稻”轮作,去年出售小龙虾每千克获得的利润为32元(利润
售价
成本).由于开发成本下降和市场供求关系变化,今年每千克小龙虾的养殖成本下降
,售价下降
,出售小龙虾每千克获得利润为30元.
(1)求去年每千克小龙虾的养殖成本与售价;
(2)该农户今年每亩农田收获小龙虾100千克,若今年的水稻种植成本为600元亩,稻谷售价为2.5元
千克,该农户估计今年可获得“虾
稻”轮作收入不少于8万元,则稻谷的亩产量至少会达到多少千克?
如图,在中,
是斜边
的中点,以
为直径作圆
交
于点
,延长
至
,使
,连接
、
,
交圆
于点
.
(1)判断四边形的形状,并说明理由;
(2)求证:;
(3)若,
,求
的长.

某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为、
、
、
、
,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 |
频率 |
0.35 |
|
0.20 |
|
0.05 |
(1)求本次调查的小型汽车数量及,
的值;
(2)补全频数分布直方图;
(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.

试题篮
()