在东西向的马路上,把出发点记为 ,向东与向西意义相反.若把向东走 记做“ ”,那么向西走 应记做( )
| A. |
|
B. |
|
C. |
|
D. |
|
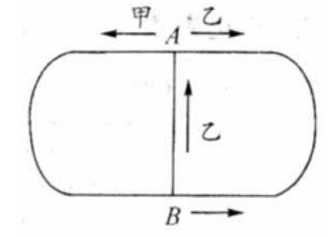
如图是一个长为 的环形跑道,其中 为跑道对称轴上的两点,且 之间有一条 的直线通道.甲乙两人同时从 点出发,甲按逆时针方向以速度 沿跑道跑步,当跑到 点时继续沿跑道前进,乙按顺时针方向以速度 沿跑道跑步,当跑到 点时沿直线通道跑回 点处,假设两人跑步的时间足够长.求:
(1)如果 ,那么甲跑了多少路程后,两人首次在 点处相遇;
(2)如果 ,那么乙跑了多少路程后,两人首次在 点处相遇.
某校九年级(1)班 名学生参加 跳绳体育考试. 跳绳次数与频数经统计后绘制出下面的频数分布表( 表示为大于等于 并且小于 )和扇形统计图,(如图).
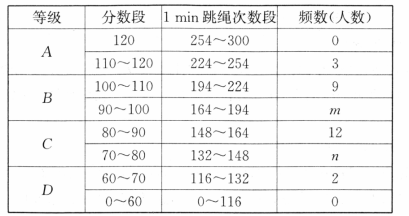
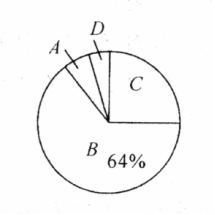
(1)求 的值;
(2)求该班 跳绳成绩在 分以上(含 分)的人数占全班人数的百分比;
(3)根据频数分布表估计该班学生 跳绳的平均分大约是多少?并说明理由.
为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙、丙三种树的价格之比为 ,丙种树每棵 元,现计划用 元资金,购买这三种树共 棵.
(1)求甲、乙两种树每棵各多少元?
(2)若购买甲种树的棵数是乙种树的 倍,恰好用完计划资金,则这三种树各能购买多少棵?
(3)若又增加了 元的购树款,在购买总棵数不变的前提下,求丙种树最多可购买多少棵?
探究:(1)如图①若 .则 .你能说明为什么吗?
(2)反之,若 ,直线 和 有什么位置关系,请证明;
(3)若将点 移至图②所示位置,此时 之间有什么关系?请证明;
(4)若将点 移至图③所示位置,情况又如何?
(5)在图④中, 与 又有何关系?
(6)在图⑤中,若 ,又得到什么结论?

已知方程: (注: 表示实数 的整数部分, 表示 的小数部分,如 ,则方程的解为_____.
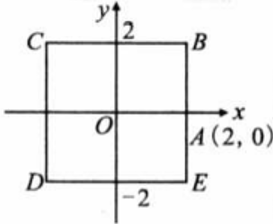
如图所示,物体 与物体 分别由点 同时出发,沿正方形 的周界做环绕运动,物体 按逆时针方向以 单位 匀速运动,物体 按顺时针方向,以 单位 匀速运动,则两个物体运动后的第 次相遇地点的坐标是_____.
在公路上,汽车 分别以每小时 的速度匀速行驶, 从甲站开往乙站, 从乙站开往甲站, 在与 相遇后两小时又与 相遇,则甲、乙两站相距_____ .
若进货价降低 而售出价不变,那么利润(按进货价而定)可由目前的 增加到 ,则原来的利润是_____.
一个水池装有 只水管,有些是进水管,有些是出水管,依次编号为①②③④⑤,分别打开两管,注满水的时间记录如下表:

要想单独打开一只水管,用最短的时间注满水池,应打开( )
| A. | ①号水管 |
B. | ②号水管 |
C. | ③号水管 |
D. | ④号或⑤号水管 |
试题篮
()