初中物理利用平衡法求液体密度试题

养生壶是一种用于养生保健的可以烹饮的容器，类似于电水壶，其最大的特点是采用一种新型的电加热材料，通过高温把电热膜电子浆料（金属化合物）喷涂在玻璃表面形成面状电阻，在两端制作银电极，通电后产生热量把壶内的水加热．小明家买了一把养生壶（图甲），其铭牌如下表所示．

型号	HX-201504
额定电压	220V
频率	50Hz
额定功率	1210W

 
小明关闭了家中的其它所有用电器，并在壶中加入初温为25℃的水，6min将水烧开（标准大气压下），求：
（1）在加热过程中家用电能表（图乙）的转盘转了300转，此过程中养生壶消耗的电能是多少？
（2）如果养生壶的热效率是87.5%，此过程中水吸收的热量是多少？
（3）壶中水的质量是多少？
（4）养生壶两端的实际电压是多少？（不考虑温度对电阻的影响）

如图所示，物体A、B均为同种材料制成的实心正方体，A的边长为10cm，B的边长为5cm，G_A=30N，则ρ_A=_________kg/m³，A对B的压强p_A=__________Pa。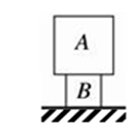

一容器装满水后，容器和水总质量为m₁；若在容器内放一质量为m的小金属块A后再加满水，总质量为m₂；若在容器内放一质量为m的小金属块A和一质量也为m的小金属块B后再加满水，总质量为m₃，则金属块A和金属块B的密度之比为

A．m2：m3

B．（m2-m1）：（m3-m1）

C．（m3-m2）：（m2-m1）

D．（m2+m-m3）：（m1+m-m2）

某空心金属球，其质量为1．5kg，球的总体积为300cm³．若将空心部分注满水后，测得总质量为1．6kg，求此金属的密度．

如图所示，体积相等、密度分别为的ρ_A、ρ_B的A、B两个立方体正对叠放在水平桌面上，且ρ_A：ρ_B=1：3．A对B的压强为p_A，B对桌面的压强为p_B．

①如果A的体积为1.0×10^﹣3米³，密度为3×10³千克/米³，求A的质量、A对B的压强．
②如果逐渐减小A的体积，但始终保持A的形状为立方体且密度不变，在A的体积逐渐减小的过程中，列出p_A与p_B的比值的表达式，并指出比值的变化规律．

龙芳同学将一重4.0N的金属筒容器，开口向上放入水中，有1/3的体积露出水面；如在筒内装入100cm³的某种液体后，金属筒有11/12的体积没入到水中；已知ρ_水＝1.0×10³kg/m³, g＝10N/kg。则金属筒的容积是        m³（筒壁厚度不计），装入金属筒内液体的密度是                kg/m³，其质量是          克。

物体A的体积是2×10^﹣3m³，将它放入水中，露出水面的体积是整个体积的四分之一，物体下表面距液面0.15m，如图所示．（g取10 N/kg）求：

（1）物体A所受的浮力是多少？
（2）物体A的密度是多大？
（3）物体下表面受到的液体压强有多大？
（4）在A上放一个多重的物体可以使A刚好全部浸入水中？

如下图所示是甲乙两种物质的质量m与体积V的关系图线。由图可知，甲乙两种物质的密度ρ_甲 、ρ_乙  关系是（ ）

A．ρ甲<ρ乙

B．ρ甲=ρ乙

C．ρ甲>ρ乙

D．无法确定

分别由不同物质a、b、c组成的三个实心体，它们的质量和体积的关系如图所示，由图可知（ ）

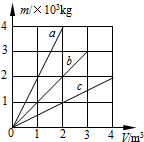
A．a物质的密度最大	B．c物质的密度最大
C．b物质的密度是2×10^3kg/m^3	D．条件不足，无法判断

图是甲、乙两种物质的质量与体积的关系图象．下列说法错误的是（ ）

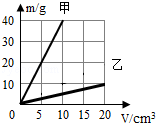
A．甲物质的质量大于乙物质的质量

B．甲物质的密度大于乙物质的密度

C．甲物质的质量与体积成正比关系

D．乙物质的密度为0.5×10^3kg/m^3

甲、乙两个铁球熔化后重新制成一个大铁球丙，则丙的密度（ ）

A．是甲、乙的密度之和	B．是甲的密度的2倍
C．和甲、乙的密度相同	D．无法确定

一辆重1×10⁴N 的汽车在水平路面匀速运动，所受阻力为920N，汽车牵引力的功率为9.2kW，其汽油发动机效率为20%（汽油热值是4.6×10⁷J/kg）．若汽车运动100s，求：
（1）牵引力做了多少功？
（2）汽车通过的距离多长？
（3）发动机消耗汽油质量是多少？

如图所示，将一个物体挂在弹簧测力计下。当物体处在空气中时，弹簧测力计的示数为50牛；把物体浸没在足够深的水中，弹簧测力计的示数为30牛。求：

（1）物体受到的浮力是多少牛？
（2）物体的体积是多大？
（3）物体的密度是多少？

如图所示的甲、乙两个实心正方体分别放在水平地面上．

①若甲的质量为1千克，求物体甲的密度ρ_甲；
②若乙的质量为2千克，求物体乙对地面的压强p_乙；
方案   设计的方法
A   加在两物体上的力方向都向下
B   加在两物体上的力方向都向上
C   甲物体上的力方向向上，乙物体上的力方向向下
D   甲物体上的力方向向下，乙物体上的力方向向上
③若甲、乙的质量分别是m、2m，底面积分别是S、nS（n＞2），要使两个正方体对水平地面的压强相等，可同时在两个正方体上表面施加一个竖直方向、大小相等的力F．某同学分别设计了如右表所示的四种方案．
选择：方案      的设计是可行的；且方案      的力F最小；
求出：可行的方案中的最小力F_小．

水平地面上有一个高为0.2米的柱状薄壁容器内放有质量为2.7千克、密度为2.7×10³千克∕米³的正方体物块，往容器内注入一定量的液体，当液面恰好与容器口相平时，液体对容器底部的压强为1960帕．求：
（1）正方体物块的体积V．
（2）容器中液体的密度ρ．
（3）当物块从液体中取出后，液体对容器底部压力减小的量△F．