已知l,m,n是空间三条直线,则下列命题正确的是( )
A.若l∥m,l∥n,则m∥n
B.若l⊥m,l⊥n,则m∥n
C.若点A、B不在直线l上,且到l的距离相等,则直线AB∥l
D.若三条直线l,m,n两两相交,则直线l,m,n共面
如图,已知菱形ACSB中,∠ABS=60°.沿着对角线SA将菱形ACSB折成三棱锥S﹣ABC,且在三棱锥S﹣ABC中,∠BAC=90°,O为BC中点.
(Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求平面ASC与平面SCB夹角的余弦值.
在梯形ABCD中,AD∥BC,BC=2AD,AD=AB= ,AB⊥BC,如图把△ABD沿BD翻折,使得平面ABD⊥平面BCD.
,AB⊥BC,如图把△ABD沿BD翻折,使得平面ABD⊥平面BCD.
(Ⅰ)求证:CD⊥平面ABD;
(Ⅱ)若点M为线段BC中点,求点M到平面ACD的距离.
给出下列命题
①若直线l与平面α内的一条直线平行,则l∥α;
②若平面α⊥平面β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β;
③∃x0∈(3,+∞),x0∉(2,+∞);
④已知a∈R,则“a<2”是“a2<2a”的必要不充分条件.
其中正确命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且E,F,G,H分别是线段PA、PD、CD、BC的中点.
(1)求证:BC∥平面EFG;
(2)DH⊥平面AEG.
已知两个不同的平面α、β和两条不重合的直线,m、n,有下列四个命题:
①若m∥n,m⊥α,则n⊥α
②若m⊥α,m⊥β,则α∥β;
③若m⊥α,m∥n,n⊂β,则α⊥β;
④若m∥α,α∩β=n,则m∥n,
其中不正确的命题的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
(1)求证:PE⊥BC;
(2)求证:EF∥平面PAD.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
(1)求证:BC⊥PB;
(2)求二面角A﹣CD﹣P的平面角的余弦值.
如图所示,在直三棱柱ABC﹣A1B1C1中,AB=BC=BB1,D为AC的中点.
(I)求证:B1C∥平面A1BD;
(Ⅱ)若AC1⊥平面A1BD,求证:B1C1⊥平面ABB1A1;
(Ⅲ)在(II)的条件下,求二面角B﹣A1C1﹣D的大小.
已知空间直角坐标系o﹣xyz中的点A的坐标为(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点,则点P的坐标满足的条件是 .
矩形 与矩形
与矩形 的公共边为
的公共边为 ,且平面
,且平面 平面
平面 ,如图所示,
,如图所示, ,
, .
.
(1)证明: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)若 是棱
是棱 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?证明你的结论.
?证明你的结论.
用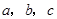 表示三条不同的直线,
表示三条不同的直线,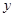 表示平面,给出下列命题,正确的是( )
表示平面,给出下列命题,正确的是( )
①若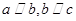 ,则
,则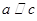 ;
;
②若 ,则
,则 ;
;
③若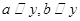 ,则
,则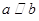 ;
;
④若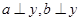 ,则
,则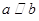 .
.
| A.①② | B.②③ | C.①④ | D.③④ |
已知 是两条不同的直线,
是两条不同的直线,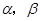 是两个不同的平面( )
是两个不同的平面( )
A.若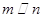 且 且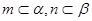 ,则 ,则 与 与 不会垂直; 不会垂直; |
B.若 是异面直线,且 是异面直线,且 , ,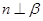 ,则 ,则 与 与 不会平行; 不会平行; |
C.若 是相交直线且不垂直, 是相交直线且不垂直,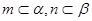 ,则 ,则 与 与 不会垂直; 不会垂直; |
D.若 是异面直线,且 是异面直线,且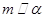 , , ,则 ,则 与 与 不会平行 不会平行 |
试题篮
()