高中数学正交试验设计方法试题

观察下面一组组合数等式：
；
；
；
…………
（1）由以上规律，请写出第个等式并证明；
（2）随机变量，求证：.

江西某品牌豆腐食品是经过、、三道工序加工而成的，、、工序的产品合格率分别为、、．已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；恰有两次合格为二等品；其它的为废品，不进入市场．
（1）生产一袋豆腐食品，求产品为废品的概率；
（2）生产一袋豆腐食品，设为三道加工工序中产品合格的工序数，求的分布列和数学期望．

设X为随机变量，X～B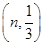，若随机变量X的数学期望E(X)＝2，则P(X＝2)等于(  )

A．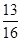

B．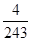

C．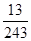

D．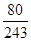

有20个零件，其中16个一等品，4个二等品，若从这20个零件中任意取3个，那么至少有1个一等品的概率是________．

甲、乙、丙三人进行乒乓球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为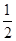，各局比赛的结果相互独立，第1局甲当裁判．
（1）求第4局甲当裁判的概率；
（2）用X表示前4局中乙当裁判的次数，求X的分布列和数学期望．

为了解某市市民对政府出台楼市限购令的态度，在该市随机抽取了50名市民进行调查，他们月收入（单位：百元）的频数分布及对楼市限购令的赞成人数如下表：

月收入		[25，35）	[35，45）
频数	5	10	15	10	5	5
赞成人数	4	8	8	5	2	1

将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收人族”。
（Ⅰ）根据已知条件完成下面的2×2列联表，有多大的把握认为赞不赞成楼市限购令与收入高低有关？
已知：，
当<2.706时，没有充分的证据判定赞不赞成楼市限购令与收入高低有关；
当>2.706时，有90％的把握判定赞不赞成楼市限购令与收入高低有关；
当>3.841时，有95％的把握判定赞不赞成楼市限购令与收入高低有关；
当>6.635时，有99％的把握判定赞不赞成楼市限购令与收入高低有关。

	非高收入族	高收入族	总计
赞成
不赞成
总计

（Ⅱ）现从月收入在[55，65）的人群中随机抽取两人，求所抽取的两人中至少一人赞成楼市限购令的概率。

某中学经市批准建设分校，工程从2010年底开工到2013年底完工，分三期完成，经过初步招标淘汰后，确定由甲、乙两建筑公司承建，且每期工程由两公司之一独立完成，必须在建完前一期工程后再建后一期工程，已知甲公司获得第一期，第二期，第三期工程承包权的概率分别是，，．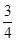
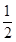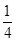(I)求甲乙两公司均至少获得l期工程的概率；
(II)求甲公司获得的工程期数的分布列和数学期望E(X)．

某足球俱乐部2013年10月份安排4次体能测试，规定：按顺序测试，一旦测试合格就不必参加以后的测试，否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为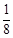的等差数列，他第一次测试合格的概率不超过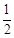，且他直到第二次测试才合格的概率为。
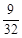（Ⅰ）求小李第一次参加测试就合格的概率P₁；
（2）求小李10月份参加测试的次数x的分布列和数学期望。

现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答.
（I）求张同学至少取到1道乙类题的概率；
（II）已知所取的3道题中有2道甲类题，1道乙类题.设张同学答对甲类题的概率都是，答对每道乙类题的概率都是，且各题答对与否相互独立.用表示张同学答对题的个数，求的分布列和数学期望.

为了研究性别不同的高中学生是否爱好某项运动,运用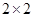列联表进行独立性检验,经计算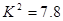,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:

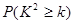	0.050	0.010	0.001
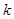	3.841	6.635	10.828

 

在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:

	科目甲	科目乙	总计
第一小组	1	5	6
第二小组	2	4	6
总计	3	9	12

现从第一小组、第二小组中各任选2人分析选课情况.
(1)求选出的4人均选科目乙的概率;
(2)设为选出的4个人中选科目甲的人数,求的分布列和数学期望.

）已知某音响设备由五个部件组成，A电视机，B影碟机，C线路，D左声道和E右声道，其中每个部件工作的概率如图所示，能听到声音，当且仅当A与B中有一个工作，C工作，D与E中有一个工作；且若D和E同时工作则有立体声效果.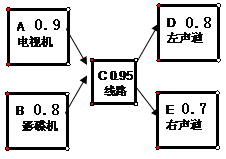

（1）求能听到立体声效果的概率；
（2）求听不到声音的概率.（结果精确到0.01）

成都市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰。若现有500人参加测试，学生成绩的频率分布直方图如下：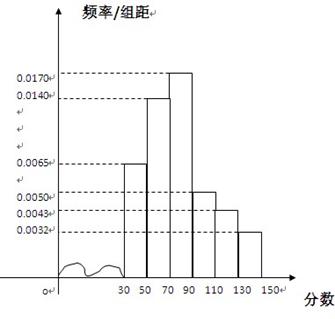

（I）求获得参赛资格的人数；
（II）根据频率直方图，估算这500名学生测试的平均成绩；
（III）若知识竞赛分初赛和复赛，在初赛中每人最多有3次选题答题的机会，累计答对2题或答错2题即终止，答对2题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为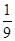，求甲通过初赛的概率.

若盒中装有同一型号的灯泡共只，其中有只合格品，只次品。
（1） 某工人师傅有放回地连续从该盒中取灯泡次，每次取一只灯泡，求次取到次品的概率；
（2） 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡，每次从中取一灯泡，若是正品则用它更换已坏灯泡，若是次品则将其报废（不再放回原盒中），求成功更换会议室的已坏灯泡所用灯泡只数的分布列和数学期望．

我校社团联即将举行一届象棋比赛，规则如下：两名选手比赛时，每局胜者得分，负者得分，比赛进行到有一人比对方多分或打满局时结束.假设选手甲与选手乙比赛时，甲每局获胜的概率皆为，且各局比赛胜负互不影响.
（Ⅰ）求比赛进行局结束，且乙比甲多得分的概率；
（Ⅱ）设表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望．