(本小题满分14分)已知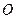 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足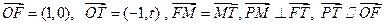 .
.
(1) 当t变化时,求点P的轨迹方程;
(2) 若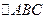 的顶点在点P的轨迹上,且点A的纵坐标
的顶点在点P的轨迹上,且点A的纵坐标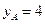 ,
,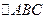 的重心恰好为点F,
的重心恰好为点F,
求直线BC的方程.
(本小题满分12分)如图所示,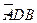 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点的直线l与曲线C相交于不同的两点M、N,问是否存在这样的直线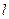 使
使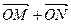 与
与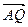 平行,若平行,求出直线
平行,若平行,求出直线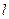 的方程, 若不平行,请说明理由.
的方程, 若不平行,请说明理由.
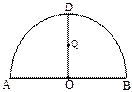
抛物线 的焦点为 ,准线为 ,经过 且斜率为 的直线与抛物线在 轴上方的部分相交于点 ,垂足为 ,则 的面积是
| A. | 4 | B. | C. | D. | 8 |
和
的极坐标方程分别为
.
(Ⅰ)把
和
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过
交点的直线的直角坐标方程.
如图,已知 是 的切线, 为切点, 是⊙O的割线,与 交于 、 两点,圆心 在 的内部,点 是 的中点.

(Ⅰ)证明
四点共圆;
(Ⅱ)求
的大小.
已知双曲线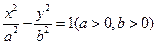 的一条渐近线方程是y=
的一条渐近线方程是y=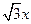 ,它的一个焦点在抛物线
,它的一个焦点在抛物线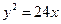 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为
A.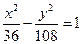 |
B.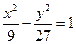  |
C.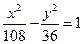 |
D.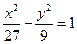 |
试题篮
()