如图,在平面直角坐标系中,矩形 的顶点 , 的坐标分别为 , .过点 的双曲线 与矩形 的边 交于点 .
(1)填空: , ,点 的坐标为 ;
(2)当 时,经过点 与点 的直线交 轴于点 ,点 是过 , 两点的抛物线 的顶点.
①当点 在双曲线 上时,求证:直线 与双曲线 没有公共点;
②当抛物线 与矩形 有且只有三个公共点,求 的值;
③当点 和点 随着 的变化同时向上运动时,求 的取值范围,并求在运动过程中直线 在四边形 中扫过的面积.

如图,在 中, , , ,动点 从点 开始沿 向点 以 的速度移动,动点 从点 开始沿 向点 以 的速度移动,若 , 两点分别从 , 两点同时出发, 点到达 点运动停止,则 的面积 随出发时间 的函数图象大致是
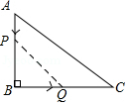
A. B.
B.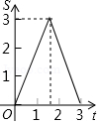
C. D.
D.
襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第 天的售价为 元 千克, 关于 的函数解析式为:
,且第12天的售价为32元 千克,第26天的售价为25元 千克.已知种植销售蓝莓的成本是18元 千克,每天的利润是 元(利润 销售收入 成本).
(1) , ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段 、折线 分别表示该有机产品每千克的销售价 (元)、生产成本 (元)与产量 之间的函数关系.
(1)求该产品销售价 (元)与产量 之间的函数关系式;
(2)直接写出生产成本 (元)与产量 之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?

飞机着陆后滑行的距离 (单位: )关于滑行时间 (单位: )的函数解析式是 .在飞机着陆滑行中,最后 滑行的距离是 .
为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第 天( ,且 为整数)每件产品的成本是 元, 与 之间符合一次函数关系,部分数据如表:
天数 |
1 |
3 |
6 |
10 |
每件成本 (元) |
7.5 |
8.5 |
10 |
12 |
任务完成后,统计发现工人李师傅第 天生产的产品件数 (件)与 (天)满足如下关系:
设李师傅第 天创造的产品利润为 元.
(1)直接写出 与 , 与 之间的函数关系式,并注明自变量 的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后,统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价 (元)和游客居住房间数 (间)的信息,乐乐绘制出 与 的函数图象如图所示:
(1)求 与 之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?

为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过 ,另外三边由 长的栅栏围成.设矩形 空地中,垂直于墙的边 ,面积为 (如图).
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)若矩形空地的面积为 ,求 的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 |
乙 |
丙 |
|
单价(元 棵) |
14 |
16 |
28 |
合理用地( 棵) |
0.4 |
1 |
0.4 |

随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了 小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养 天后的质量为 ,销售单价为 元 ,根据往年的行情预测, 与 的函数关系为 , 与 的函数关系如图所示.
(1)设每天的养殖成本为 元,收购成本为 元,求 与 的值;
(2)求 与 的函数关系式;
(3)如果将这批小龙虾放养 天后一次性出售所得利润为 元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?
(总成本 放养总费用 收购成本;利润 销售总额 总成本)

我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量 (万件)与月份 (月)的关系为: ,每件产品的利润 (元)与月份 (月)的关系如下表:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
10 |
10 |
(1)请你根据表格求出每件产品利润 (元)与月份 (月)的关系式;
(2)若月利润 (万元) 当月销售量 (万件) 当月每件产品的利润 (元),求月利润 (万元)与月份 (月)的关系式;
(3)当 为何值时,月利润 有最大值,最大值为多少?
新欣商场经营某种新型电子产品,购进时的价格为20元 件.根据市场预测,在一段时间内,销售价格为40元 件时,销售量为200件,销售单价每降低1元,就可多售出20件.
(1)写出销售量 (件)与销售单价 (元)之间的函数关系式;
(2)写出销售该产品所获利润 (元)与销售单价 (元)之间的函数关系式,并求出商场获得的最大利润;
(3)若商场想获得不低于4000元的利润,同时要完成不少于320件的该产品销售任务,该商场应该如何确定销售价格.
正方形 的边长为1,点 是 边上的一个动点(与 , 不重合),以 为顶点在 所在直线的上方作 .
(1)当 经过点 时,
①请直接填空: (可能,不可能)过 点;(图1仅供分析)
②如图2,在 上截取 ,过 点作 垂直于直线 ,垂足为点 ,作 于 ,求证:四边形 为正方形.
(2)当 不过点 时,设 交边 于 ,且 .在 上存在点 ,过 点作 垂直于直线 ,垂足为点 ,使得 ,连接 ,求四边形 的最大面积.

为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为 的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为 ,种草所需费用 (元)与 的函数关系式为 ,其图象如图所示:栽花所需费用 (元 与 的函数关系式为 .
(1)请直接写出 、 和 的值;
(2)设这块 空地的绿化总费用为 (元),请利用 与 的函数关系式,求出绿化总费用 的最大值;
(3)若种草部分的面积不少于 ,栽花部分的面积不少于 ,请求出绿化总费用 的最小值.

飞机着陆后滑行的距离 (单位:米)关于滑行的时间 (单位:秒)的函数解析式是 ,则飞机着陆后滑行的最长时间为 秒.
试题篮
()