初中数学二次函数的应用试题

某种商品每件进价为20元，调查表明：在某段时间内若以每件 $x$元 $(20⩽x⩽30$，且 $x$为整数）出售，可卖出 $(30-x)$件，若使利润最大，则每件商品的售价应为　　元．

如图，在 $\mathit{\Delta ABC}$中， $\angle B=90°$， $\tan \angle C=\frac{3}{4}$， $\mathit{AB}=6\mathit{cm}$．动点 $P$从点 $A$开始沿边 $\mathit{AB}$向点 $B$以 $1\mathit{cm}/s$的速度移动，动点 $Q$从点 $B$开始沿边 $\mathit{BC}$向点 $C$以 $2\mathit{cm}/s$的速度移动．若 $P$， $Q$两点分别从 $A$， $B$两点同时出发，在运动过程中， $\mathit{\Delta PBQ}$的最大面积是 $($　　 $)$

A． $18c{m}^2$B． $12c{m}^2$C． $9c{m}^2$D． $3c{m}^2$

草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量 $y$ （千克）与销售单价 $x$ （元）符合一次函数关系，如图是 $y$ 与 $x$ 的函数关系图象．

（1）求 $y$ 与 $x$ 的函数解析式（也称关系式）；

（2）设该水果销售店试销草莓获得的利润为 $W$ 元，求 $W$ 的最大值．

已知：如图，四边形 $\mathit{ABCD}$， $\mathit{AB}//\mathit{DC}$， $\mathit{CB}\perp \mathit{AB}$， $\mathit{AB}=16\mathit{cm}$， $\mathit{BC}=6\mathit{cm}$， $\mathit{CD}=8\mathit{cm}$，动点 $P$从点 $D$开始沿 $\mathit{DA}$边匀速运动，动点 $Q$从点 $A$开始沿 $\mathit{AB}$边匀速运动，它们的运动速度均为 $2\mathit{cm}/s$．点 $P$和点 $Q$同时出发，以 $\mathit{QA}$、 $\mathit{QP}$为边作平行四边形 $\mathit{AQPE}$，设运动的时间为 $t\left(s\right)$， $0<t<5$．

根据题意解答下列问题：

（1）用含 $t$的代数式表示 $\mathit{AP}$；

（2）设四边形 $\mathit{CPQB}$的面积为 $S\left(c{m}^2\right)$，求 $S$与 $t$的函数关系式；

（3）当 $\mathit{QP}\perp \mathit{BD}$时，求 $t$的值；

（4）在运动过程中，是否存在某一时刻 $t$，使点 $E$在 $\angle \mathit{ABD}$的平分线上？若存在，求出 $t$的值；若不存在，请说明理由．

某公司投入研发费用80万元 $(80$万元只计入第一年成本），成功研发出一种产品．公司按订单生产（产量 $=$销售量），第一年该产品正式投产后，生产成本为6元 $/$件．此产品年销售量 $y$（万件）与售价 $x$（元 $/$件）之间满足函数关系式 $y=-x+26$．

（1）求这种产品第一年的利润 $W_1$（万元）与售价 $x$（元 $/$件）满足的函数关系式；

（2）若该产品第一年的利润为20万元，那么该产品第一年的售价是多少？

（3）在（2）的条件下，第二年，该公司将第一年的利润20万元 $(20$万元只计入第二年成本）再次投入研发，使产品的生产成本降为5元 $/$件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润 $W_2$至少为多少万元．

一列自然数0，1，2，3， $\dots$，100．依次将该列数中的每一个数平方后除以100，得到一列新数．则下列结论正确的是 $($　　 $)$

A．原数与对应新数的差不可能等于零

B．原数与对应新数的差，随着原数的增大而增大

C．当原数与对应新数的差等于21时，原数等于30

D．当原数取50时，原数与对应新数的差最大

知识背景

当 $a>0$且 $x>0$时，因为 ${(\sqrt{x}-\frac{\sqrt{a}}{\sqrt{x}})}^2⩾0$，所以 $x-2\sqrt{a}+\frac{a}{x}⩾0$，从而 $x+\frac{a}{x}⩾2\sqrt{a}$（当 $x=\sqrt{a}$时取等号）．

设函数 $y=x+\frac{a}{x}(a>0,x>0)$，由上述结论可知：当 $x=\sqrt{a}$时，该函数有最小值为 $2\sqrt{a}$．

应用举例

已知函数为 $y_1=x(x>0)$与函数 $y_2=\frac{4}{x}(x>0)$，则当 $x=\sqrt{4}=2$时， $y_1+y_2=x+\frac{4}{x}$有最小值为 $2\sqrt{4}=4$．

解决问题

（1）已知函数 $y_1=x+3(x>-3)$与函数 $y_2={(x+3)}^2+9(x>-3)$，当 $x$取何值时， $\frac{y_2}{y_1}$有最小值？最小值是多少？

（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001．若设该设备的租赁使用天数为 $x$天，则当 $x$取何值时，该设备平均每天的租货使用成本最低？最低是多少元？

如图所示，已知 $\mathit{\Delta ABC}$中， $\mathit{BC}=12$， $\mathit{BC}$边上的高 $h=6$， $D$为 $\mathit{BC}$上一点， $\mathit{EF}//\mathit{BC}$，交 $\mathit{AB}$于点 $E$，交 $\mathit{AC}$于点 $F$，设点 $E$到边 $\mathit{BC}$的距离为 $x$．则 $\mathit{\Delta DEF}$的面积 $y$关于 $x$的函数图象大致为 $($　　 $)$

A．B．

C．D．

如图，一小球沿与地面成一定角度的方向飞出，小球的飞行路线是一条抛物线．如果不考虑空气阻力，小球的飞行高度 $y$（单位： $m)$与飞行时间 $x$（单位： $s)$之间具有函数关系 $y=-5x^2+20x$，请根据要求解答下列问题：

（1）在飞行过程中，当小球的飞行高度为 $15m$时，飞行时间是多少？

（2）在飞行过程中，小球从飞出到落地所用时间是多少？

（3）在飞行过程中，小球飞行高度何时最大？最大高度是多少？

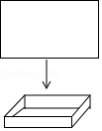
工人师傅用一块长为 $10\mathit{dm}$，宽为 $6\mathit{dm}$的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

（1）在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为 $12d{m}^2$时，裁掉的正方形边长多大？

（2）若要求制作的长方体的底面长不大于底面宽的五倍，并在容器外表面进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？

如图，在 $\mathit{\Delta ABC}$中， $\angle C=90°$， $\mathit{AB}=10\mathit{cm}$， $\mathit{BC}=8\mathit{cm}$，点 $P$从点 $A$沿 $\mathit{AC}$向点 $C$以 $1\mathit{cm}/s$的速度运动，同时点 $Q$从点 $C$沿 $\mathit{CB}$向点 $B$以 $2\mathit{cm}/s$的速度运动（点 $Q$运动到点 $B$停止），在运动过程中，四边形 $\mathit{PABQ}$的面积最小值为 $($　　 $)$

A． $19c{m}^2$B． $16c{m}^2$C． $15c{m}^2$D． $12c{m}^2$

已知： $\text{Rt}\Delta \text{EFP}$和矩形 $\mathit{ABCD}$如图①摆放（点 $P$与点 $B$重合），点 $F$， $B\left(P\right)$， $C$在同一直线上， $\mathit{AB}=\mathit{EF}=6\mathit{cm}$， $\mathit{BC}=\mathit{FP}=8\mathit{cm}$， $\angle \mathit{EFP}=90°$．如图②， $\mathit{\Delta EFP}$从图①的位置出发，沿 $\mathit{BC}$方向匀速运动，速度为 $1\mathit{cm}/s$， $\mathit{EP}$与 $\mathit{AB}$交于点 $G$；同时，点 $Q$从点 $C$出发，沿 $\mathit{CD}$方向匀速运动，速度为 $1\mathit{cm}/s$．过点 $Q$作 $\mathit{QM}\perp \mathit{BD}$，垂足为 $H$，交 $\mathit{AD}$于点 $M$，连接 $\mathit{AF}$， $\mathit{PQ}$，当点 $Q$停止运动时， $\mathit{\Delta EFP}$也停止运动．设运动时间为 $t\left(s\right)(0<t<6)$，解答下列问题：

（1）当 $t$为何值时， $\mathit{PQ}//\mathit{BD}$？

（2）设五边形 $\mathit{AFPQM}$的面积为 $y\left(c{m}^2\right)$，求 $y$与 $t$之间的函数关系式；

（3）在运动过程中，是否存在某一时刻 $t$，使 $S_{\mathit{五边形AFPQM}}:S_{\mathit{矩形ABCD}}=9:8$？若存在，求出 $t$的值；若不存在，请说明理由．

（4）在运动过程中，是否存在某一时刻 $t$，使点 $M$在线段 $\mathit{PG}$的垂直平分线上？若存在，求出 $t$的值；若不存在，请说明理由．

青岛市某大酒店豪华间实行淡季、旺季两种价格标准，旺季每间价格比淡季上涨 $\frac{1}{3}$．下表是去年该酒店豪华间某两天的相关记录：

	淡季	旺季
未入住房间数	10	0
日总收入（元 $)$	24000	40000

（1）该酒店豪华间有多少间？旺季每间价格为多少元？

（2）今年旺季来临，豪华间的间数不变．经市场调查发现，如果豪华间仍旧实行去年旺季价格，那么每天都客满；如果价格继续上涨，那么每增加25元，每天未入住房间数增加1间．不考虑其他因素，该酒店将豪华间的价格上涨多少元时，豪华间的日总收入最高？最高日总收入是多少元？

足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度 $h$（单位： $m)$与足球被踢出后经过的时间 $t$（单位： $s)$之间的关系如下表：

$t$	0	1	2	3	4	5	6	7	$\dots$
$h$	0	8	14	18	20	20	18	14	$\dots$

下列结论：①足球距离地面的最大高度为 $20m$；②足球飞行路线的对称轴是直线 $t=\frac{9}{2}$；③足球被踢出 $9s$时落地；④足球被踢出 $1.5s$时，距离地面的高度是 $11m$．其中正确结论的个数是 $($　　 $)$

A．1B．2C．3D．4

某商店经销一种双肩包，已知这种双肩包的成本价为每个30元．市场调查发现，这种双肩包每天的销售量 $y$（单位：个）与销售单价 $x$（单位：元）有如下关系： $y=-x+60(30⩽x⩽60)$．

设这种双肩包每天的销售利润为 $w$元．

（1）求 $w$与 $x$之间的函数解析式；

（2）这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？

（3）如果物价部门规定这种双肩包的销售单价不高于48元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元？