(1)如图1,菱形的顶点
、
在菱形
的边上,且
,请直接写出
的结果(不必写计算过程)
(2)将图1中的菱形绕点
旋转一定角度,如图2,求
;
(3)把图2中的菱形都换成矩形,如图3,且,此时
的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.

如图,正方形 ABCD ,点 F 在边 AB 上,且 AF:FB=1:2 , CE⊥DF ,垂足为 M ,且交 AD 于点 E , AC 与 DF 交于点 N ,延长 CB 至 G ,使 BG=12BC ,连接 GM .有如下结论:① DE=AF ;② AN=√24AB ;③ ∠ADF=∠GMF ;④ SΔANF:S四边形CNFB=1:8 .上述结论中,所有正确结论的序号是 ( )

| A. |
①② |
B. |
①③ |
C. |
①②③ |
D. |
②③④ |
如图,矩形中,点
在边
上,将
沿
折叠,点
落在
边上的点
处,过点
作
交
于点
,连接
.
(1)求证:四边形是菱形;
(2)若,
,求四边形
的面积.

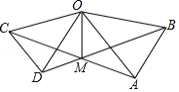
如图,在 ΔOAB 和 ΔOCD 中, OA=OB , OC=OD , OA>OC , ∠AOB=∠COD=40° ,连接 AC , BD 交于点 M ,连接 OM .下列结论:① AC=BD ;② ∠AMB=40° ;③ OM 平分 ∠BOC ;④ MO 平分 ∠BMC .其中正确的个数为 ( )
| A. |
4 |
B. |
3 |
C. |
2 |
D. |
1 |
(1)如图1,是正方形
边
上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①线段和
的数量关系是 ;
②写出线段,
和
之间的数量关系.
(2)当四边形为菱形,
,点
是菱形
边
所在直线上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①如图2,点在线段
上时,请探究线段
、
和
之间的数量关系,写出结论并给出证明;
②如图3,点在线段
的延长线上时,
交射线
于点
,若
,
,直接写出线段
的长度.

在矩形中,连结
,点
从点
出发,以每秒1个单位的速度沿着
的路径运动,运动时间为
(秒
.过点
作
于点
,在矩形
的内部作正方形
.
(1)如图,当时,
①若点在
的内部,连结
、
,求证:
;
②当时,设正方形
与
的重叠部分面积为
,求
与
的函数关系式;
(2)当,
时,若直线
将矩形
的面积分成
两部分,求
的值.

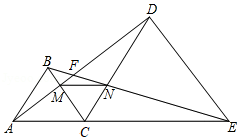
如图,和
都是等边三角形,且点
、
、
在同一直线上,
与
、
分别交于点
、
,
与
交于点
.下列结论正确的是 (写出所有正确结论的序号).
①;②
;③
;④
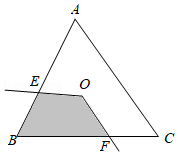
如图, ∠EOF 的顶点 O 是边长为2的等边 ΔABC 的重心, ∠EOF 的两边与 ΔABC 的边交于 E , F , ∠EOF=120° ,则 ∠EOF 与 ΔABC 的边所围成阴影部分的面积是 ( )
| A. |
√32 |
B. |
2√35 |
C. |
√33 |
D. |
√34 |
已知二次函数的图象过点
,点
与
不重合)是图象上的一点,直线
过点
且平行于
轴.
于点
,点
.
(1)求二次函数的解析式;
(2)求证:点在线段
的中垂线上;
(3)设直线交二次函数的图象于另一点
,
于点
,线段
的中垂线交
于点
,求
的值;
(4)试判断点与以线段
为直径的圆的位置关系.
如图,的对角线
、
相交于点
,
经过
,分别交
、
于点
、
,
的延长线交
的延长线于
.
(1)求证:;
(2)若,
,
,求
的长.

如图,在正方形 ABCD 中, E 是 BC 边上的一点, BE=4 , EC=8 ,将正方形边 AB 沿 AE 折叠到 AF ,延长 EF 交 DC 于 G ,连接 AG , FC ,现在有如下4个结论:
① ∠EAG=45° ;② FG=FC ;③ FC//AG ;④ SΔGFC=14 .
其中正确结论的个数是 ( )

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
试题篮
()