初中数学等腰三角形的判定试题

如图，直线 $l_1//l_2$ ，点 $A$ 在直线 $l_1$ 上，以点 $A$ 为圆心，适当长为半径画弧，分别交直线 $l_1$ ， $l_2$ 于 $B$ ， $C$ 两点，连接 $\mathit{AC}$ ， $\mathit{BC}$ ，若 $\angle \mathit{ABC}=54°$ ，则 $\angle 1$ 的度数为 $($ 　　 $)$

A．

$36°$

B．

$54°$

C．

$72°$

D．

$73°$

如图，在中，，是上一点，经过点、、，交于点，过点作，交于点．

求证：（1）四边形是平行四边形；

（2）．

已知 $\angle \mathit{AOB}$ ，作 $\angle \mathit{AOB}$ 的平分线 $\mathit{OM}$ ，在射线 $\mathit{OM}$ 上截取线段 $\mathit{OC}$ ，分别以 $O$ 、 $C$ 为圆心，大于 $\frac{1}{2}\mathit{OC}$ 的长为半径画弧，两弧相交于 $E$ ， $F$ ．画直线 $\mathit{EF}$ ，分别交 $\mathit{OA}$ 于 $D$ ，交 $\mathit{OB}$ 于 $G$ ．那么 $\mathit{\Delta ODG}$ 一定是 $($ 　　 $)$

A．

锐角三角形

B．

钝角三角形

C．

等腰三角形

D．

直角三角形

实践操作：

第一步：如图1，将矩形纸片 $\mathit{ABCD}$ 沿过点 $D$ 的直线折叠，使点 $A$ 落在 $\mathit{CD}$ 上的点 $A^{\text{'}}$ 处，得到折痕 $\mathit{DE}$ ，然后把纸片展平．

第二步：如图2，将图1中的矩形纸片 $\mathit{ABCD}$ 沿过点 $E$ 的直线折叠，点 $C$ 恰好落在 $\mathit{AD}$ 上的点 $C\text{'}$ 处，点 $B$ 落在点 $B^{\text{'}}$ 处，得到折痕 $\mathit{EF}$ ， $B^{\text{'}}C\text{'}$ 交 $\mathit{AB}$ 于点 $M$ ， $C\text{'}F$ 交 $\mathit{DE}$ 于点 $N$ ，再把纸片展平．

问题解决：

（1）如图1，填空：四边形 $\mathit{AE}{A}^{\text{'}}D$ 的形状是 　 　；

（2）如图2，线段 $\mathit{MC}\text{'}$ 与 $\mathit{ME}$ 是否相等？若相等，请给出证明；若不等，请说明理由；

（3）如图2，若 $\mathit{AC}\text{'}=2\mathit{cm}$ ， $D{C}^{\text{'}}=4\mathit{cm}$ ，求 $\mathit{DN}:\mathit{EN}$ 的值．

（1）如图（1），已知与交于点，，．求证：．

（2）如图（2），已知的延长线与交于点，，．探究与的数量关系，并说明理由．

如图，在 $\mathit{\Delta ABC}$ 中，点 $D$ ， $E$ 分别是 $\mathit{AB}$ 、 $\mathit{AC}$ 边上的点， $\mathit{BD}=\mathit{CE}$ ， $\angle \mathit{ABE}=\angle \mathit{ACD}$ ， $\mathit{BE}$ 与 $\mathit{CD}$ 相交于点 $F$ ．求证： $\mathit{\Delta ABC}$ 是等腰三角形．

如图，抛物线为常数，与轴交于，两点，点为抛物线的顶点，点的坐标为，，连接并延长与过，，三点的相交于点．

（1）求点的坐标；

（2）过点作的切线交轴于点．

①如图1，求证：；

②如图2，连接，，，当，时，求的值．

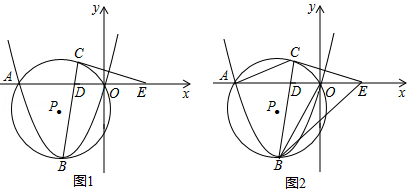
抛物线与轴交于点，（点在点的左边），与轴交于点，点是该抛物线的顶点．

（1）如图1，连接，求线段的长；

（2）如图2，点是直线上方抛物线上一点，轴于点，与线段交于点；将线段沿轴左右平移，线段的对应线段是，当的值最大时，求四边形周长的最小值，并求出对应的点的坐标；

（3）如图3，点是线段的中点，连接，将沿直线翻折至△的位置，再将△绕点旋转一周，在旋转过程中，点，的对应点分别是点，，直线分别与直线，轴交于点，．那么，在△的整个旋转过程中，是否存在恰当的位置，使是以为腰的等腰三角形？若存在，请直接写出所有符合条件的线段的长；若不存在，请说明理由．

如图，在菱形中，，，点是这个菱形内部或边上的一点，若以点、、为顶点的三角形是等腰三角形，则、、两点不重合）两点间的最短距离为　　．

如图，是的直径，于点，连接交于点，过点作的切线交于点，连接交于点．

（1）求证：；

（2）连接并延长，交于点．填空：

①当的度数为　　时，四边形为菱形；

②当的度数为　　时，四边形为正方形．

如图，在中，，以为直径的交边于点，过点作，与过点的切线交于点，连接．

（1）求证：；

（2）若，，求的长．

如图，四边形 $\mathit{ABCD}$ 是平行四边形， $\mathit{AE}$ 平分 $\angle \mathit{BAD}$ ，交 $\mathit{DC}$ 的延长线于点 $E$ ．求证： $\mathit{DA}=\mathit{DE}$ ．

如图，已知的中垂线交于点，交于点，有下面3个结论：

①是等腰三角形；
②∽；
③点D是线段AC的黄金分割点．
请你从以上结论中只选一个加以证明

如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线相交于点E，∠ADC＝60°．

（1）求证：△ADE是等腰三角形；
（2）若AD＝2，求BE的长．