初中数学平行线分线段成比例试题

如图，已知一次函数的图像与轴，轴分别交于A（1，0）、B（0，－1）两点，且又与反比例函数的图像在第一象限交于C点，C点的横坐标为2.
⑴求一次函数的解析式；
⑵求C点坐标及反比例函数的解析式.

如图，已知直线l经过点A(1，0)，与双曲线y＝

(x＞0)交于点B(2，1)．过点P(p，p－1)(p＞1)作x轴的平
行线分别交双曲线y＝(x＞0)和y＝－(x＜0)于点M、N．
(1)求m的值和直线l的解析式；
(2)若点P在直线y＝2上，求证：△PMB∽△PNA；
(3)是否存在实数p，使得S_△AMN＝4S_△AMP？若存在，请求出所有满足条件的p的值；若
不存在，请说明理由．

在平面直角坐标系xOy中，已知反比例函数满足：当x＜0时，y随x的增大而减小．若该反比例函数的图象与直线都经过点P，且，则实数k=___________

如图，已知反比例函数的图象经过点（，8），直线y=﹣x+b经过该反比例函数图象上的点Q（4，m）．
（1）求上述反比例函数和直线的函数表达式；
（2）设该直线与x轴、y轴分别相交于A、B两点，与反比例函数图象的另一个交点为P，连接0P、OQ，求△OPQ的面积．

如图，□ABCD的顶点A，B的坐标分别是A（-1，0），B（0，-2），顶点C，D在双曲线y=上，边AD交y轴于点E，且四边形BCDE的面积是△ABE面积的5倍，则k=_____.

如图，面积为8的矩形ABOC的边OB、OC分别在轴、轴的正半
轴上，点A在双曲线的图象上，且AC=2．
（1）求值；
（2）将矩形ABOC以B旋转中心，顺时针旋转90°后得到矩形FBDE，双曲线交DE于M点，交EF于N点，求△MEN的面积．
(3)在双曲线上是否存在一点P，使得直线PN与直线BC平行？若存在，请求出P点坐标，若不存在，请说明理由．

如图，在△ABO中，已知A(0，4)，B(－2，0)， D为线段AB的中点.
（1）求点D的坐标；
（2）求经过点D的反比例函数解析式.

如图，已知直线y=﹣2x经过点P（﹣2，a），点P关于y轴的对称点P′在反比例函数（k≠0）的图象上．
（1）求a的值；
（2）直接写出点P′的坐标；
（3）求反比例函数的解析式．

(本小题8分)已知一次函数(b为常数)的图象与反比例函数（k为常数．且）的图象相交于点P(3．1)．
(I) 求这两个函数的解析式；
(II) 当x>3时，试判断与的大小．井说明理由。

如图，一次函数y=k₁x+b的图象经过A（0，﹣2），B（1，0）两点，与反比例函数的图象在第一象限内的交点为M，若△OBM的面积为2．
（1）求一次函数和反比例函数的表达式；
（2）在x轴上是否存在点P，使AM⊥MP？若存在，求出点P的坐标；若不存在，说明理由．

．根据图5中①所示的程序，得到了y与x的函数图象，如图5中②，若点M是
y轴正半轴上任意一点，过点M作PQ∥x轴交图象于点P、Q，连接OP、OQ，则以下结论：

①x＜0时，y=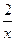
②△OPQ的面积为定值
③x＞0时，y随x的增大而增大 
④MQ=2PM
⑤∠POQ可以等于90°
其中正确结论是
A．①②④           B．②④⑤           C．③④⑤           D．②③⑤

已知点(1，1)在反比例函数y＝(k为常数，k≠0)的图象上，则这个反比例函数的大致图象是

．如果反比例函数（k是常数，k≠0）的图像经过点(－1，2)，那么这个函数的解析式是__________．      

若A(x₁，y₁)，B(x₂，y₂），C(x₃，y₃)是反比例函数y=图象上的点，且x₁＜x₂
＜0＜x₃，则y₁、y₂、y₃的大小关系正确的是                                  (      )                                               
A  y₃＞y₁＞y₂   B  y₁＞y₂＞y₃   C  y₂＞y₁＞y₃    D  y₃＞y₂＞y₁

已知点在反比例函数的图象上，若点P关于y轴对称的点在反比例函数的图象上，则k的值为       .