初中数学解直角三角形的应用试题

如图，1号楼在2号楼的南侧，两楼高度均为 $90m$，楼间距为 $\mathit{AB}$．冬至日正午，太阳光线与水平面所成的角为 $32.3°$，1号楼在2号楼墙面上的影高为 $\mathit{CA}$；春分日正午，太阳光线与水平面所成的角为 $55.7°$，1号楼在2号楼墙面上的影高为 $\mathit{DA}$．已知 $\mathit{CD}=42m$．

（1）求楼间距 $\mathit{AB}$；

（2）若2号楼共30层，层高均为 $3m$，则点 $C$位于第几层？（参考数据： $\sin 32.3°\approx 0.53$， $\cos 32.3°\approx 0.85$， $\tan 32.3°\approx 0.63$， $\sin 55.7°\approx 0.83$， $\cos 55.7°\approx 0.56$， $\tan 55.7°\approx 1.47)$

京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点 $A$、 $B$和点 $C$、 $D$，先用卷尺量得 $\mathit{AB}=160m$， $\mathit{CD}=40m$，再用测角仪测得 $\angle \mathit{CAB}=30°$， $\angle \mathit{DBA}=60°$，求该段运河的河宽（即 $\mathit{CH}$的长）．

图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框上，通过推动左侧活页门开关．图2是其俯视简化示意图，已知轨道 $\mathit{AB}=120\mathit{cm}$，两扇活页门的宽 $\mathit{OC}=\mathit{OB}=60\mathit{cm}$，点 $B$固定，当点 $C$在 $\mathit{AB}$上左右运动时， $\mathit{OC}$与 $\mathit{OB}$的长度不变．（所有的结果保留小数点后一位）

（1）若 $\angle \mathit{OBC}=50°$，求 $\mathit{AC}$的长；

（2）当点 $C$从点 $A$向右运动 $60\mathit{cm}$时，求点 $O$在此过程中运动的路径长．

参考数据： $\sin 50°\approx 0.77$． $\cos 50°\approx 0.64$， $\tan 50°\approx 1.19$， $\pi$取3.14．

图1是一辆吊车的实物图，图2是其工作示意图， $\mathit{AC}$是可以伸缩的起重臂，其转动点 $A$离地面 $\mathit{BD}$的高度 $\mathit{AH}$为 $3.4m$．当起重臂 $\mathit{AC}$长度为 $9m$，张角 $\angle \mathit{HAC}$为 $118°$时，求操作平台 $C$离地面的高度（结果保留小数点后一位：参考数据： $\sin 28°\approx 0.47$， $\cos 28°\approx 0.88$， $\tan 28°\approx 0.53)$

如图1，窗框和窗扇用“滑块铰链”连接，图3是图2中“滑块铰链”的平面示意图，滑轨 $\mathit{MN}$安装在窗框上，托悬臂 $\mathit{DE}$安装在窗扇上，交点 $A$处装有滑块，滑块可以左右滑动，支点 $B$， $C$， $D$始终在一直线上，延长 $\mathit{DE}$交 $\mathit{MN}$于点 $F$．已知 $\mathit{AC}=\mathit{DE}=20\mathit{cm}$， $\mathit{AE}=\mathit{CD}=10\mathit{cm}$， $\mathit{BD}=40\mathit{cm}$．

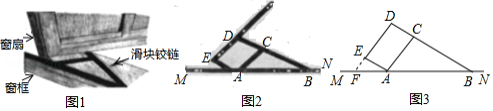
（1）窗扇完全打开，张角 $\angle \mathit{CAB}=85°$，求此时窗扇与窗框的夹角 $\angle \mathit{DFB}$的度数；

（2）窗扇部分打开，张角 $\angle \mathit{CAB}=60°$，求此时点 $A$， $B$之间的距离（精确到 $0.1\mathit{cm})$．

（参考数据： $\sqrt{3}\approx 1.732$， $\sqrt{6}\approx 2.449)$

如图，两根竹竿 $\mathit{AB}$和 $\mathit{AD}$斜靠在墙 $\mathit{CE}$上，量得 $\angle \mathit{ABC}=\alpha$， $\angle \mathit{ADC}=\beta$，则竹竿 $\mathit{AB}$与 $\mathit{AD}$的长度之比为 $($　　 $)$

A． $\frac{\tan \alpha }{\tan \beta }$B． $\frac{\sin \beta }{\sin \alpha }$C． $\frac{\sin \alpha }{\sin \beta }$D． $\frac{\cos \beta }{\cos \alpha }$

如图是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧 $\mathit{OB}$与墙 $\mathit{MN}$平行且距离为0.8米．已知小汽车车门宽 $\mathit{AO}$为1.2米，当车门打开角度 $\angle \mathit{AOB}$为 $40°$时，车门是否会碰到墙？请说明理由．（参考数据： $\sin 40°\approx 0.64$； $\cos 40°\approx 0.77$； $\tan 40°\approx 0.84)$

如图，一名滑雪运动员沿着倾斜角为 $34°$的斜坡，从 $A$滑行至 $B$，已知 $\mathit{AB}=500$米，则这名滑雪运动员的高度下降了　　米．（参考数据： $\sin 34°\approx 0.56$， $\cos 34°\approx 0.83$， $\tan 34°\approx 0.67)$

如图是某小区的一个健身器材，已知 $\mathit{BC}=0.15m$， $\mathit{AB}=2.70m$， $\angle \mathit{BOD}=70°$，求端点 $A$到地面 $\mathit{CD}$的距离（精确到 $0.1m)$．（参考数据： $\sin 70°\approx 0.94$， $\cos 70°\approx 0.34$， $\tan 70°\approx 2.75)$

如图是小强洗漱时的侧面示意图，洗漱台（矩形 $\mathit{ABCD})$靠墙摆放，高 $\mathit{AD}=80\mathit{cm}$，宽 $\mathit{AB}=48\mathit{cm}$，小强身高 $166\mathit{cm}$，下半身 $\mathit{FG}=100\mathit{cm}$，洗漱时下半身与地面成 $80°(\angle \mathit{FGK}=80°)$，身体前倾成 $125°(\angle \mathit{EFG}=125°)$，脚与洗漱台距离 $\mathit{GC}=15\mathit{cm}$（点 $D$， $C$， $G$， $K$在同一直线上）．

（1）此时小强头部 $E$点与地面 $\mathit{DK}$相距多少？

（2）小强希望他的头部 $E$恰好在洗漱盆 $\mathit{AB}$的中点 $O$的正上方，他应向前或后退多少？

$(\sin 80°\approx 0.98$， $\cos 80°\approx 0.17$， $\sqrt{2}\approx 1.41$，结果精确到 $0.1)$

保护视力要求人写字时眼睛和笔端的距离应超过 $30\mathit{cm}$，图1是一位同学的坐姿，把他的眼睛 $B$，肘关节 $C$和笔端 $A$的位置关系抽象成图2的 $\mathit{\Delta ABC}$，已知 $\mathit{BC}=30\mathit{cm}$， $\mathit{AC}=22\mathit{cm}$， $\angle \mathit{ACB}=53°$，他的这种坐姿符合保护视力的要求吗？请说明理由．（参考数据： $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6$， $\tan 53°\approx 1.3)$

一座楼梯的示意图如图所示， $\mathit{BC}$是铅垂线， $\mathit{CA}$是水平线， $\mathit{BA}$与 $\mathit{CA}$的夹角为 $\theta$．现要在楼梯上铺一条地毯，已知 $\mathit{CA}=4$米，楼梯宽度1米，则地毯的面积至少需要 $($　　 $)$

A． $\frac{4}{\sin \theta }$米 ${}^2$B． $\frac{4}{\cos \theta }$米 ${}^2$C． $(4+\frac{4}{\tan \theta })$米 ${}^2$D． $(4+4\tan \theta )$米 ${}^2$

太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面 $\mathit{\Delta ABC}$如图2所示， $\mathit{BC}=10$米， $\angle \mathit{ABC}=\angle \mathit{ACB}=36°$，改建后顶点 $D$在 $\mathit{BA}$的延长线上，且 $\angle \mathit{BDC}=90°$，求改建后南屋面边沿增加部分 $\mathit{AD}$的长．（结果精确到0.1米）

（参考数据： $\sin 18°\approx 0.31$， $\cos 18°\approx 0.95$． $\tan 18°\approx 0.32$， $\sin 36°\approx 0.59$． $\cos 36°\approx 0.81$， $\tan 36°\approx 0.73)$

如图是小红在一次放风筝活动中某时段的示意图，她在 $A$处时的风筝线（整个过程中风筝线近似地看作直线）与水平线构成 $30°$角，线段 $A{A}_1$表示小红身高1.5米．

（1）当风筝的水平距离 $\mathit{AC}=18$米时，求此时风筝线 $\mathit{AD}$的长度；

（2）当她从点 $A$跑动 $9\sqrt{2}$米到达点 $B$处时，风筝线与水平线构成 $45°$角，此时风筝到达点 $E$处，风筝的水平移动距离 $\mathit{CF}=10\sqrt{3}$米，这一过程中风筝线的长度保持不变，求风筝原来的高度 $C_{1}D$．

某小区为了安全起见，决定将小区内的滑滑板的倾斜角由 $45°$调为 $30°$，如图，已知原滑滑板 $\mathit{AB}$的长为4米，点 $D$， $B$， $C$在同一水平地面上，调整后滑滑板会加长多少米？（结果精确到0.01米，参考数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732$， $\sqrt{6}\approx 2.449)$