若 a>1,则双曲线 y 2=1的离心率的取值范围是( )
| A. |
( ,+∞) |
B. |
( ,2) |
C. |
(1, ) |
D. |
(1,2) |
设非零向量 , 满足| |=| |则( )
| A. | ⊥ |
B. | | |=| | |
C. | ∥ |
D. | | |>| | |
函数 f( x)=sin(2 x )的最小正周期为( )
| A. |
4π |
B. |
2π |
C. |
π |
D. |
|
(1+ i)(2+ i)=( )
| A. |
1﹣i |
B. |
1+3i |
C. |
3+i |
D. |
3+3i |
设集合 A={1,2,3}, B={2,3,4},则 A∪ B=( )
| A. |
{1,2,3,4} |
B. |
{1,2,3} |
C. |
{2,3,4} |
D. |
{1,3,4} |
[选修4―4:坐标系与参数方程]
在直角坐标系 中,曲线 C的参数方程为 ,直线 l的参数方程为 .
(1)若 ,求 C与 l的交点坐标;
(2)若 C上的点到 l的距离的最大值为 ,求a.
已知椭圆C: ,四点P1(1,1),P2(0,1),P3 ,P4 中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布 .
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在 之外的零件数,求 及 的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得
,
,其中
为抽取的第
 个零件的尺寸,
.
个零件的尺寸,
.
用样本平均数 作为 的估计值 ,用样本标准差 作为 的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计 和 (精确到0.01).
附:若随机变量 服从正态分布 ,则 ,
, .
如图,在四棱锥 中, ,且 .
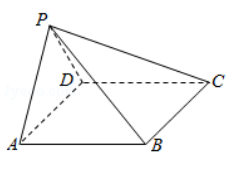
(1)证明:平面 平面 ;
(2)若 , ,求二面角 的余弦值.
△ABC的内角A,B,C的对边分别为a,b,c,已知 的面积为
(1)求 ;
(2)若 , ,求 的周长.
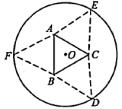
如图,圆形纸片的圆心为 O,半径为5 cm,该纸片上的等边三角形 ABC的中心为 O。 D、 E、 F为圆 O上的点, , , 分别是以 BC, CA, AB为底边的等腰三角形。沿虚线剪开后,分别以 BC, CA, AB为折痕折起 , , ,使得 D、 E、 F重合,得到三棱锥。当 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为 .
已知双曲线C: 的右顶点为A,以A为圆心,b为半径做圆A,圆A与双曲线C的一条渐近线交于M、N两点。若 ,则C的离心率为 .
几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了"解数学题获取软件激活码"的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是2 0,接下来的两项是2 0,2 1,再接下来的三项是2 0,2 1,2 2, 依此类推 . 求满足如下条件的 & 最小整数 且该数列的前 N 项和为 2 的整数 幂 . 那么该款软件的激活码是( )
| A. |
440 |
B. |
330 |
C. |
220 |
D. |
110 |
试题篮
()