高中数学试题

已知点P(0，1)，椭圆+y²=m(m>1)上两点A，B满足 $\stackrel{⃑}{\mathit{AP}}$=2 $\stackrel{⃑}{\mathit{PB}}$，则当m=___________时，点B横坐标的绝对值最大．

从1，3，5，7，9中任取2个数字，从0，2，4，6中任取2个数字，一共可以组成___________个没有重复数字的四位数.(用数字作答)

二项式 $(\sqrt[3]{x}+\frac{1}{2x}{)}^8$的展开式的常数项是___________．

已知λ∈R，函数f(x)= $\left\{\begin{array}{c}x-4,x\ge \lambda \\ x^2-4x+3,x<\lambda \end{array}\right.$，当λ=2时，不等式f(x)<0的解集是___________．若函数f(x)恰有2个零点，则λ的取值范围是___________．

在△ABC中，角A，B，C所对的边分别为a，b，c．若 $a=\sqrt{7}$，b=2，A=60°，则sin B=___________，c=___________．

若 $x,y$满足约束条件 $\left\{\begin{array}{c}x-y\ge 0,\\ 2x+y\le 6,\\ x+y\ge 2,\end{array}\right.$则的最小值是___________，最大值是___________．

已知 成等比数列，且 $a_1+a_2+a_3+a_4=\mathit{ln}(a_1+a_2+a_3)$ ．若 ，则（    ）

A．

$a_1<a_3,a_2<a_4$

B．

$a_1>a_3,a_2<a_4$

C．

$a_1<a_3,a_2>a_4$

D．

$a_1>a_3,a_2>a_4$

已知 $\stackrel{⃑}{a}$ 、 $\stackrel{⃑}{b}$ 、 $\stackrel{⃑}{e}$ 是平面向量， $\stackrel{⃑}{e}$ 是单位向量．若非零向量 $\stackrel{⃑}{a}$ 与 $\stackrel{⃑}{e}$ 的夹角为 $\frac{\pi }{3}$ ，向量 $\stackrel{⃑}{b}$ 满足 ${\stackrel{⃑}{b}}^2-4\stackrel{⃑}{e}\cdot \stackrel{⃑}{b}+3=0$ ，则 $\left|\stackrel{⃑}{a}-\stackrel{⃑}{b}\right|$ 的最小值是（    ）

A．

$\sqrt{3}-1$

B．

$\sqrt{3}+1$

C．

2

D．

$2-\sqrt{3}$

已知四棱锥 $S-\mathit{ABCD}$ 的底面是正方形，侧棱长均相等， $E$ 是线段 $\mathit{AB}$ 上的点（不含端点），设 $\mathit{SE}$ 与 $\mathit{BC}$ 所成的角为 ${\theta }_1$ ， $\mathit{SE}$ 与平面 $\mathit{ABCD}$ 所成的角为 ${\theta }_2$ ，二面角 $S-\mathit{AB}-C$ 的平面角为 ${\theta }_3$ ，则（    ）

A．

${\theta }_1\le {\theta }_2\le {\theta }_3$

B．

${\theta }_3\le {\theta }_2\le {\theta }_1$

C．

${\theta }_1\le {\theta }_3\le {\theta }_2$

D．

${\theta }_2\le {\theta }_3\le {\theta }_1$

设 $0<p<1$ ，随机变量 $\xi$ 的分布列如图，则当 $p$ 在 $\left(0,1\right)$ 内增大时，（    ）

$\xi$	$0$	$1$	$2$
$P$	$\frac{1-p}{2}$	$\frac{1}{2}$	$\frac{p}{2}$

A．	$D\left(\xi \right)$ 减小	B．	$D\left(\xi \right)$ 增大
C．	$D\left(\xi \right)$ 先减小后增大	D．	$D\left(\xi \right)$ 先增大后减小

在直角坐标系 $\mathit{xOy}$中，曲线 $C_1$的方程为 $y=k\left|x\right|+2$.以坐标原点为极点， $x$轴正半轴为极轴建立极坐标系，曲线 $C_2$的极坐标方程为 ${\rho }^2+2\rho \mathit{cos}\theta -3=0$.

（1）求 $C_2$的直角坐标方程；

（2）若 $C_1$与 $C_2$有且仅有三个公共点，求 $C_1$的方程.

已知函数 $f\left(x\right)=a{e}^x-\mathit{lnx}-1$．

（1）设 $x=2$是 $f\left(x\right)$的极值点．求 $a$，并求 $f\left(x\right)$的单调区间；

（2）证明：当 $a\ge \frac{1}{e}$时， $f\left(x\right)\ge 0$．

设抛物线 $C：\mathit{\hspace{0.33em}\hspace{0.33em}}{y}^2=2x$，点 $A\left(2\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}0\right)$， $B\left(-2\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}0\right)$，过点 $A$的直线 $l$与 $C$交于 $M$， $N$两点．

（1）当 $l$与 $x$轴垂直时，求直线 $\mathit{BM}$的方程；

（2）证明： $\angle \mathit{ABM}=\angle \mathit{ABN}$．

某家庭记录了未使用节水龙头 $50$ 天的日用水量数据（单位： $m^3$ ）和使用了节水龙头 $50$ 天的日用水量数据，得到频数分布表如下：

未使用节水龙头 $50$ 天的日用水量频数分布表

日用水量	$[0,0.1)$	$[0.1,0.2)$	$[0.2,0.3)$	$[0.3,0.4)$	$[0.4,0.5)$	$[0.5,0.6)$	$[0.6,0.7)$
频数	$1$	$3$	$2$	$4$	$9$	$26$	$5$

使用了节水龙头 $50$ 天的日用水量频数分布表

日用水量	$[0,0.1)$	$[0.1,0.2)$	$[0.2,0.3)$	$[0.3,0.4)$	$[0.4,0.5)$	$[0.5,0.6)$
频数	$1$	$5$	$13$	$10$	$16$	$5$

（1）在答题卡上作出使用了节水龙头 $50$ 天的日用水量数据的频率分布直方图：

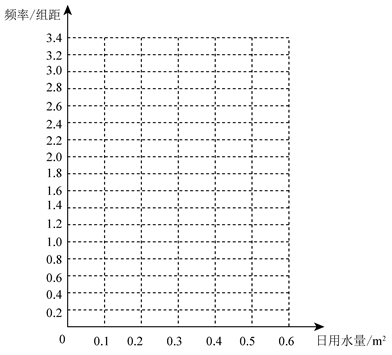
（2）估计该家庭使用节水龙头后，日用水量小于 $0.35m^3$ 的概率；

（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按 $365$ 天计算，同一组中的数据以这组数据所在区间中点的值作代表．）

如图，在平行四边形 $\mathit{ABCM}$ 中， $\mathit{AB}=\mathit{AC}=3$ ， $\angle \mathit{ACM}=90°$ ，以 $\mathit{AC}$ 为折痕将△ $\mathit{ACM}$ 折起，使点 $M$ 到达点 $D$ 的位置，且 ．

（1）证明：平面 $\mathit{ACD}\perp$ 平面 $\mathit{ABC}$ ；

（2） $Q$ 为线段 $\mathit{AD}$ 上一点， $P$ 为线段 $\mathit{BC}$ 上一点，且 ，求三棱锥 的体积．