高中数学试题

在长方体 $\mathit{ABCD}-A_1{B}_1{C}_1{D}_1$ 中， $\mathit{AB}=\mathit{BC}=1$ ， $A{A}_1=\sqrt{3}$ ，则异面直线 $A{D}_1$ 与 $D{B}_1$ 所成角的余弦值为（    ）

A．

$\frac{1}{5}$

B．

$\frac{\sqrt{5}}{6}$

C．

$\frac{\sqrt{5}}{5}$

D．

$\frac{\sqrt{2}}{2}$

在平面直角坐标系 $\mathit{xOy}$中， $\odot O$的参数方程为 $\left\{\begin{array}{c}x=\mathit{cos}\theta ，\\ y=\mathit{sin}\theta \end{array}\right.$（ $\theta$为参数），过点 $\left(0\hspace{0.33em}，-\sqrt{2}\right)$且倾斜角为 $\alpha$的直线 $l$与 $\odot O$交于 $A\hspace{0.33em}，\hspace{0.33em}B$两点．

（1）求 $\alpha$的取值范围；

（2）求 $\mathit{AB}$中点 $P$的轨迹的参数方程．

如图，边长为2的正方形 $\mathit{ABCD}$ 所在的平面与半圆弧 $\stackrel{⏜}{\mathit{CD}}$ 所在平面垂直， $M$ 是 $\stackrel{⏜}{\mathit{CD}}$ 上异于 $C$ ， $D$ 的点．

（1）证明：平面 $\mathit{AMD}\perp$ 平面 $\mathit{BMC}$ ；

（2）当三棱锥 $M-\mathit{ABC}$ 体积最大时，求面 $\mathit{MAB}$ 与面 $\mathit{MCD}$ 所成二面角的正弦值．

某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：

（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；

（2）求40名工人完成生产任务所需时间的中位数 $m$，并将完成生产任务所需时间超过 $m$和不超过 $m$的工人数填入下面的列联表：

	超过 $m$	不超过 $m$
第一种生产方式
第二种生产方式

（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？

附： $K^2=\frac{n{\left(\mathit{ad}-\mathit{bc}\right)}^2}{\left(a+b\right)\left(c+d\right)\left(a+c\right)\left(b+d\right)}$，

已知点 $M\left(-1，1\right)$和抛物线 $C：y^2=4x$，过 $C$的焦点且斜率为 $k$的直线与 $C$交于 $A$， $B$两点．若 $\angle \mathit{AMB}=90°$，则 $k=$________．

设 $a={\mathit{log}}_{0.2}0.3$ ， $b={\mathit{log}}_{2}0.3$ ，则(   )

A．	$a+b<\mathit{ab}<0$	B．	$\mathit{ab}<a+b<0$
C．	$a+b<0<\mathit{ab}$	D．	$\mathit{ab}<0<a+b$

设 $F_1$ , $F_2$ 是双曲线 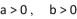（ ）的左、右焦点， $O$ 是坐标原点．过 $F_2$ 作 $C$ 的一条渐近线的垂线，垂足为 $P$ ．若 $\left|P{F}_1\right|=\sqrt{6}\left|\mathit{OP}\right|$ ，则 $C$ 的离心率为(   )

A．

$\sqrt{5}$

B．

$\sqrt{3}$

C．

$2$

D．

$\sqrt{2}$

$△\mathit{ABC}$ 的内角 $\mathit{A\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}B\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}C}$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $△\mathit{ABC}$ 的面积为 $\frac{a^2+b^2-c^2}{4}$ ，则 $C=$ (   )

A．

$\frac{\pi }{2}$

B．

$\frac{\pi }{3}$

C．

$\frac{\pi }{4}$

D．

$\frac{\pi }{6}$

某群体中的每位成员使用移动支付的概率都为 $p$ ，各成员的支付方式相互独立，设 $X$ 为该群体的10位成员中使用移动支付的人数， $\mathit{DX}=2.4$ ， $P\left(X=4\right)<P\left(X=6\right)$ ，则 $p=$ (   )

A．

0.7

B．

0.6

C．

0.4

D．

0.3

函数 $y=-x^4+x^2+2$ 的图像大致为(   )

A．		B．
C．		D．

直线 $x+y+2=0$ 分别与 $x$ 轴， $y$ 轴交于 $A$ ， $B$ 两点，点 $P$ 在圆 ${\left(x-2\right)}^2+y^2=2$ 上，则 $△\mathit{ABP}$ 面积的取值范围是(   )

A．

$\left[2\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}6\right]$

B．

$\left[4\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}8\right]$

C．

$\left[\sqrt{2}\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}3\sqrt{2}\right]$

D．

$\left[2\sqrt{2}\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}3\sqrt{2}\right]$

如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y ²=4x上存在不同的两点A，B满足PA，PB的中点均在C上．

（Ⅰ）设AB中点为M，证明：PM垂直于y轴；

（Ⅱ）若P是半椭圆x ²+ $\frac{y^2}{4}$ =1(x<0)上的动点，求△PAB面积的取值范围．

已知等比数列{a_n}的公比q>1，且a₃+a₄+a₅=28，a₄+2是a₃，a₅的等差中项．数列{b_n}满足b₁=1，数列{（b_n+1−b_n）a_n}的前n项和为2n²+n．

（Ⅰ）求q的值；

（Ⅱ）求数列{b_n}的通项公式．

如图，已知多面体ABC-A ₁B ₁C ₁，A ₁A，B ₁B，C ₁C均垂直于平面ABC，∠ABC=120°，A ₁A=4，C ₁C=1，AB=BC=B ₁B=2．

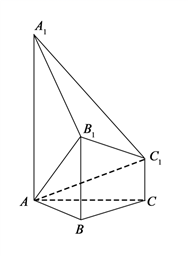
（Ⅰ）证明：AB ₁⊥平面A ₁B ₁C ₁；

（Ⅱ）求直线AC ₁与平面ABB ₁所成的角的正弦值．

已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（ $-\frac{3}{5}，-\frac{4}{5}$）．

（Ⅰ）求sin（α+π）的值；

（Ⅱ）若角β满足sin（α+β）= $\frac{5}{13}$，求cosβ的值．