高中数学试题

已知数列 $\left\{a_n\right\}$满足 $a_1=1$， $n{a}_{n+1}=2\left(n+1\right)a_n$，设 $b_n=\frac{a_n}{n}$．

（1）求 $b_1\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}{b}_2\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}{b}_3$；

（2）判断数列 $\left\{b_n\right\}$是否为等比数列，并说明理由；

（3）求 $\left\{a_n\right\}$的通项公式．

△ $\mathit{ABC}$的内角 $\mathit{A\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}B\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}C}$的对边分别为 $\mathit{a\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}b\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}c}$，已知 $b\text{sin}C+c\text{sin}B=4a\text{sin}B\text{sin}C$， $b^2+c^2-a^2=8$，则△ $\mathit{ABC}$的面积为________．

直线 $y=x+1$与圆 $x^2+y^2+2y-3=0$交于 $\mathit{A\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}B}$两点，则 $\left|\mathit{AB}\right|=$________．

若 $x$， $y$满足约束条件 $\left\{\begin{array}{c}x-2y-2\le 0\\ x-y+1\ge 0\\ y\le 0\end{array}\right.$，则 $z=3x+2y$的最大值为_____________．

设函数 $f\left(x\right)=\left\{\begin{array}{c}{2}^{-x}，x\le 0\\ 1，x>0\end{array}\right.$ ，则满足 $f\left(x+1\right)<f\left(2x\right)$ 的 x的取值范围是（ ）

A．

$(-\infty ,-1]$

B．

$\left(0，+\infty \right)$

C．

$\left(-1，0\right)$

D．

$\left(-\infty ，0\right)$

已知角 $\alpha$ 的顶点为坐标原点，始边与 $x$ 轴的非负半轴重合，终边上有两点 $A\left(1，a\right)$ ， $B\left(2，b\right)$ ，且 $\text{cos}2\alpha =\frac{2}{3}$ ，则 $\left|a-b\right|=$ （  ）

A．

$\frac{1}{5}$

B．

$\frac{\sqrt{5}}{5}$

C．

$\frac{2\sqrt{5}}{5}$

D．

$1$

在长方体 $\mathit{ABCD}-A_1{B}_1{C}_1{D}_1$ 中， $\mathit{AB}=\mathit{BC}=2$ ， $A{C}_1$ 与平面 $B{B}_1{C}_{1}C$ 所成的角为 $30^{\circ }$ ，则该长方体的体积为（   ）

A．

$8$

B．

$6\sqrt{2}$

C．

$8\sqrt{2}$

D．

$8\sqrt{3}$

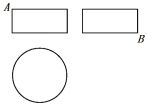
某圆柱的高为2，底面周长为16，其三视图如图所示，圆柱表面上的点 $M$ 在正视图上的对应点为 $A$ ，圆柱表面上的点 $N$ 在左视图上的对应点为 $B$ ，则在此圆柱侧面上，从 $M$ 到 $N$ 的路径中，最短路径的长度为（   ）

A．

$2\sqrt{17}$

B．

$2\sqrt{5}$

C．

$3$

D．

2

已知函数 $f\left(x\right)=2{\mathit{cos}}^{2}x-{\mathit{sin}}^{2}x+2$ ，则（   ）

A．	$f\left(x\right)$ 的最小正周期为 $\pi$ ，最大值为 $3$
B．	$f\left(x\right)$ 的最小正周期为 $\pi$ ，最大值为 $4$
C．	$f\left(x\right)$ 的最小正周期为 $2\pi$ ，最大值为 $3$
D．	$f\left(x\right)$ 的最小正周期为 $2\pi$ ，最大值为 $4$

在△ $\mathit{ABC}$ 中， $\mathit{AD}$ 为 $\mathit{BC}$ 边上的中线， $E$ 为 $\mathit{AD}$ 的中点，则 $\stackrel{⃑}{\mathit{EB}}=$ （   ）

A．	$\frac{3}{4}\stackrel{⃑}{\mathit{AB}}-\frac{1}{4}\stackrel{⃑}{\mathit{AC}}$	B．	$\frac{1}{4}\stackrel{⃑}{\mathit{AB}}-\frac{3}{4}\stackrel{⃑}{\mathit{AC}}$
C．	$\frac{3}{4}\stackrel{⃑}{\mathit{AB}}+\frac{1}{4}\stackrel{⃑}{\mathit{AC}}$	D．	$\frac{1}{4}\stackrel{⃑}{\mathit{AB}}+\frac{3}{4}\stackrel{⃑}{\mathit{AC}}$

设函数 $f\left(x\right)=x^3+\left(a-1\right)x^2+\mathit{ax}$ ．若 $f\left(x\right)$ 为奇函数，则曲线 在点 $\left(0，0\right)$ 处的切线方程为(　　)

A．

$y=-2x$

B．

$y=-x$

C．

$y=2x$

D．

$y=x$

在直角坐标系 $\mathit{xOy}$中，曲线 $C$的参数方程为 $\left\{\begin{array}{c}x=2\mathit{cos\theta }\\ y=4\mathit{sin\theta }\end{array}\right.$（ $\theta$为参数），直线 $l$的参数方程为 $\left\{\begin{array}{c}x=1+\mathit{tcos\alpha }\\ y=2+\mathit{tsin\alpha }\end{array}\right.$（ $t$为参数）.

（1）求 $C$和 $l$的直角坐标方程；

（2）若曲线 $C$截直线 $l$所得线段的中点坐标为 $\left(1,2\right)$，求 $l$的斜率．

已知函数 $f\left(x\right)=\frac{1}{3}{x}^3-a\left(x^2+x+1\right)$．

（1）若 $a=3$，求 $f\left(x\right)$的单调区间；

（2）证明： $f\left(x\right)$只有一个零点．

设抛物线 $C：\mathit{\hspace{0.33em}\hspace{0.33em}}{y}^2=4x$ 的焦点为 $F$ ，过 $F$ 且斜率为 $k(k>0)$ 的直线 $l$ 与 $C$ 交于 $A$ ， $B$ 两点， $\left|\mathit{AB}\right|\hspace{0.33em}=8$ ．

（1）求 $l$ 的方程；

（2）求过点 $A$ ， $B$ 且与 $C$ 的准线相切的圆的方程．

如图，在三棱锥 $P-\mathit{ABC}$ 中， $\mathit{AB}=\mathit{BC}=2\sqrt{2}$ ， $\mathit{PA}=\mathit{PB}=\mathit{PC}=\mathit{AC}=4$ ， $O$ 为 $\mathit{AC}$ 的中点．

（1）证明： $\mathit{PO}\perp$ 平面 $\mathit{ABC}$ ；

（2）若点 $M$ 在棱 $\mathit{BC}$ 上，且 $\mathit{MC}=2\mathit{MB}$ ，求点 $C$ 到平面 $\mathit{POM}$ 的距离．