如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=30米,并在点C测得塔顶A的仰角为60°,则塔高AB= 米.

已知椭圆C: +
+ =1(a>b>0)的两个焦点分别为F1(﹣2,0),F2(2,0),离心率为
=1(a>b>0)的两个焦点分别为F1(﹣2,0),F2(2,0),离心率为 .过焦点F2的直线l(斜率不为0)与椭圆C交于A,B两点,线段AB的中点为D,O为坐标原点,直线OD交椭圆于M,N两点.
.过焦点F2的直线l(斜率不为0)与椭圆C交于A,B两点,线段AB的中点为D,O为坐标原点,直线OD交椭圆于M,N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当四边形MF1NF2为矩形时,求直线l的方程.
已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为 .
某程序框图如图所示,执行该程序后输出的S的值是( )

A. |
B. |
C.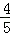 |
D. |
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
下列五个命题中:
①函数y=loga(2x﹣1)+2015(a>0且a≠1)的图象过定点(1,2015);
②若定义域为R函数f(x)满足:对任意互不相等的x1、x2都有(x1﹣x2)[f(x1)﹣f(x2)]>0,则f(x)是减函数;
③f(x+1)=x2﹣1,则f(x)=x2﹣2x;
④若函数f(x)= 是奇函数,则实数a=﹣1;
是奇函数,则实数a=﹣1;
⑤若a= (c>0,c≠1),则实数a=3.
(c>0,c≠1),则实数a=3.
其中正确的命题是 .(填上相应的序号).
设函数f(x)=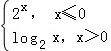 ,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
| A.1 | B.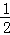 |
C. |
D.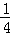 |
已知集合M{h(x)|h(x)的定义域为R,且对任意x都有h(﹣x)=﹣h(x)}设函数f(x)= (a,b为常数).
(a,b为常数).
(1)当a=b=1时,判断是否有f(x)∈M,说明理由;
(2)若函数f(x)∈M,且对任意的x都有f(x)<sinθ成立,求θ的取值范围.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.
试题篮
()