已知函数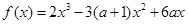
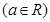 .
.
(1)当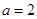 时,求函数
时,求函数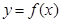 的单调区间;
的单调区间;
(2)若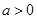 时,函数
时,函数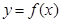 在闭区间
在闭区间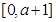 上的最大值为
上的最大值为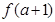 ,求
,求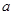 的取值范围.
的取值范围.
已知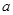 为实常数,函数
为实常数,函数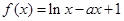 .
.
(1)讨论函数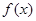 的单调性;
的单调性;
(2)若函数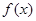 有两个不同的零点
有两个不同的零点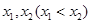 ;
;
(Ⅰ)求实数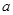 的取值范围;
的取值范围;
(Ⅱ)求证: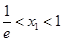 且
且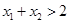 .(注:
.(注: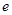 为自然对数的底数)
为自然对数的底数)
已知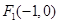 、
、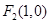 为椭圆
为椭圆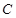 的左、右焦点,且点
的左、右焦点,且点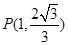 在椭圆
在椭圆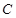 上.
上.
(1)求椭圆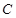 的方程;
的方程;
(2)过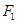 的直线
的直线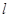 交椭圆
交椭圆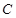 于
于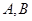 两点,则
两点,则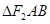 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值?
若存在其最大值及此时的直线方程;若不存在,请说明理由.
数列 的首项为
的首项为 (
( ),前
),前 项和为
项和为 ,且
,且 (
( ).设
).设 ,
, (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)当 时,若对任意
时,若对任意 ,
, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)当 时,试求三个正数
时,试求三个正数 ,
, ,
,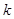 的一组值,使得
的一组值,使得 为等比数列,且
为等比数列,且 ,
, ,
,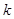 成等差数列.
成等差数列.
已知函数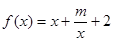 (
( 为实常数).
为实常数).
(1)若函数 图像上动点
图像上动点 到定点
到定点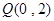 的距离的最小值为
的距离的最小值为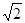 ,求实数
,求实数 的值;
的值;
(2)若函数 在区间
在区间 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数 的取值范围;
的取值范围;
(3)设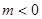 ,若不等式
,若不等式 在
在 有解,求
有解,求 的取值范围.
的取值范围.
如图,已知抛物线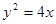 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.
(1)求证:KF平分∠MKN;
(2)O为坐标原点,直线MO、NO分别交准线于点P、Q,求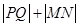 的最小值.
的最小值.
已知函数 .
.
(I) 当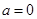 ,求
,求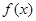 的最小值;
的最小值;
(II) 若函数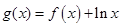 在区间
在区间 上为增函数,求实数
上为增函数,求实数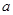 的取值范围;
的取值范围;
(III)过点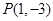 恰好能作函数
恰好能作函数 图象的两条切线,并且两切线的倾斜角互补,求实数
图象的两条切线,并且两切线的倾斜角互补,求实数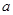 的取值范围.
的取值范围.
已知函数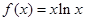 .
.
(I)求函数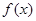 的单调递减区间;
的单调递减区间;
(II)若 在
在 上恒成立,求实数
上恒成立,求实数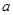 的取值范围;
的取值范围;
(III)过点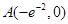 作函数
作函数 图像的切线,求切线方程
图像的切线,求切线方程
已知函数 .
.
(1)若函数满足 ,且在定义域内
,且在定义域内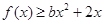 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(2)若函数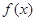 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数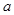 的取值范围;
的取值范围;
(3)当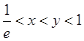 时,试比较
时,试比较 与
与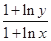 的大小.
的大小.
已知函数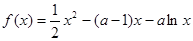 ,
,
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 在区间
在区间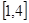 内的最小值为
内的最小值为 ,求
,求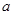 的值.(参考数据
的值.(参考数据 )
)
已知函数f(x)的导函数为f ′(x),且对任意x>0,都有f ′(x)> .
.
(Ⅰ)判断函数F(x)= 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(Ⅱ)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)请将(Ⅱ)中的结论推广到一般形式,并证明你所推广的结论.
在平面直角坐标系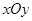 中,已知椭圆
中,已知椭圆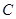 :
: 的离心率
的离心率 ,且椭圆C上一点
,且椭圆C上一点 到点Q
到点Q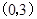 的距离最大值为4,过点
的距离最大值为4,过点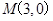 的直线交椭圆
的直线交椭圆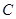 于点
于点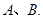
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆上一点,且满足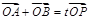 (O为坐标原点),当
(O为坐标原点),当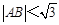 时,求实数
时,求实数 的取值范围.
的取值范围.
已知函数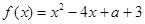 ,
,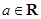 .
.
(Ⅰ)若函数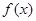 在
在 上至少有一个零点,求
上至少有一个零点,求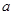 的取值范围;
的取值范围;
(Ⅱ)若函数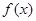 在
在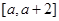 上的最大值为
上的最大值为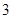 ,求
,求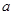 的值.
的值.
试题篮
()