高中数学试题

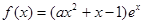已知函数，其中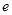是自然对数的底数，．
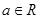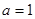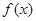（1）若，求曲线在点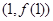处的切线方程；
（2）若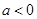，求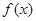的单调区间；
（3）若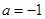，函数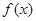的图象与函数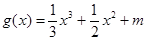的图象有3个不同的交点，求实数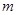的取值范围.

已知数列满足，.
(1)求证：数列是等比数列；
(2)设，求数列的前项和；
(3)设，数列的前项和为，求证：(其中).

已知等比数列的首项，公比，设数列的通项公式，数列，的前项和分别记为，，试比较与的大小.

若不等式对恒成立，则实数的取值范围是       .

如图所示，一个半圆和长方形组成的铁皮，长方形的边为半圆的直径，为半圆的圆心，，，现要将此铁皮剪出一个等腰三角形，其底边.

（1）设，求三角形铁皮的面积；
（2）求剪下的铁皮三角形的面积的最大值.

已知函数．
（Ⅰ）若函数在区间上存在极值，求实数的取值范围；
（Ⅱ）如果当时，不等式恒成立，求实数的取值范围，并且判断代数式的大小．

已知幂函数的图象与x轴，y轴无交点且关于原点对称，又有函数f(x)=x²－alnx+m－2在(1，2]上是增函数，g(x)=x－在(0,1)上为减函数.
①求a的值；
②若，数列{a_n}满足a₁＝1，a_n+1＝p(a_n)，（n∈N₊），数列{b_n}，满足，，求数列{a_n}的通项公式a_n和s_n.
③设，试比较[h(x)]ⁿ+2与h(xⁿ)+2ⁿ的大小（n∈N₊），并说明理由.

已知、分别是椭圆: 的左、右焦点，点在直线上，线段的垂直平分线经过点．直线与椭圆交于不同的两点、，且椭圆上存在点，使，其中是坐标原点，是实数．
（Ⅰ）求的取值范围；
（Ⅱ）当取何值时，的面积最大？最大面积等于多少？

给定椭圆： ，称圆心在原点，半径为的圆是椭圆的“准圆”．若椭圆的一个焦点为，且其短轴上的一个端点到的距离为.
(Ⅰ)求椭圆的方程和其“准圆”方程；
(Ⅱ)点是椭圆的“准圆”上的一个动点，过动点作直线，使得与椭圆都只有一个交点，试判断是否垂直，并说明理由．

(本小题满分12分）有一种密码，明文是由三个字符组成，密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排取一个字符组成，且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排成一排组成.

第一排	明文字符	A	B	C	D
密码字符	11	12	13	14
第二排	明文字符	E	F	G	H
密码字符	21	22	23	24
第三排	明文字符	M	N	P	Q
密码字符	1	2	3	4

设随机变量表示密码中不同数字的个数．
(Ⅰ)求；   (Ⅱ)求随机变量的分布列和它的数学期望．

已知函数，，（1）若，求函数的极值；
（2）若函数在上单调递减，求实数的取值范围；
（3）在函数的图象上是否存在不同的两点，使线段的中点的横坐标与直线的斜率之间满足？若存在，求出；若不存在，请说明理由.

已知二次函数，且不等式的解集为.
（1）方程有两个相等的实根，求的解析式；
（2）的最小值不大于，求实数的取值范围；
（3）如何取值时，函数存在零点，并求出零点.

已知数列中，，，若数列满足.
（Ⅰ）证明：数列是等差数列，并写出的通项公式；
（Ⅱ）求数列的通项公式及数列中的最大项与最小项.

如图,已知曲线,曲线,P是平面上一点,若存在过点P的直线与都有公共点,则称P为“C₁—C₂型点”.

(1)在正确证明的左焦点是“C₁—C₂型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线与有公共点,求证,进而证明原点不是“C₁—C₂型点”;
(3)求证:圆内的点都不是“C₁—C₂型点”.

（Ⅰ）已知函数,若存在，使得,则称是函数的一个不动点，设二次函数.
(Ⅰ) 当时，求函数的不动点；
(Ⅱ) 若对于任意实数，函数恒有两个不同的不动点，求实数的取值范围；
(Ⅲ) 在(Ⅱ)的条件下，若函数的图象上两点的横坐标是函数的不动点，且直线是线段的垂直平分线，求实数的取值范围.