若 ,则“
,则“ 成立”是“
成立”是“ 成立”的 条件(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).
成立”的 条件(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).
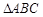 中,角
中,角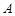 ,
,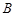 的对边分别为
的对边分别为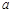 ,
,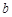 ,则“
,则“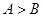 ”是“
”是“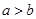 ”的 条件(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).
”的 条件(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).
下列四个结论中,①命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1”;②若p∧q为假命题,则p,q均为假命题;③若命题p:∃x0∈R,使得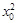 +2x0+3<0,则﹁p: ∀x∈R,都有x2+2x+3≥0;④设a,b为两个非零向量,则“a·b=|a|·|b|”是“a与b共线”的充分必要条件;正确结论的序号是的是_____.
+2x0+3<0,则﹁p: ∀x∈R,都有x2+2x+3≥0;④设a,b为两个非零向量,则“a·b=|a|·|b|”是“a与b共线”的充分必要条件;正确结论的序号是的是_____.
下列结论:
①若命题p:∃x0∈R,tan x0=2;命题q:∀x∈R,x2-x+ >0.则命题“p∧(
>0.则命题“p∧( q)”是假命题;
q)”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是 =-3;
=-3;
③“设a、b∈R,若ab≥2,则a2+b2>4”的否命题为:“设a、b∈R,若ab<2,则a2+b2≤4”.
其中正确结论的序号为________.
在△ABC中,“ ”是“
”是“ ”的 条件.(填“充分”、“必要”、“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
”的 条件.(填“充分”、“必要”、“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
已知p:(x-1)(y-2)=0,q:(x-1)2+(y-2)2=0,则p是q的________条件
下列四种说法:
①命题“ ,使得
,使得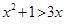 ”的否定是“
”的否定是“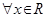 ,都有
,都有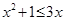 ”;
”;
②设 、
、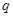 是简单命题,若“
是简单命题,若“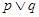 ”为假命题,则“
”为假命题,则“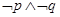 ” 为真命题;
” 为真命题;
③若 是
是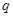 的充分不必要条件,则
的充分不必要条件,则 的必要不充分条件;
的必要不充分条件;
④把函数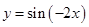
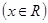 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数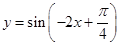
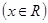 的图像.
的图像.
其中所有正确说法的序号是 .
常用逻辑用语“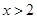 ”是“
”是“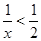 ”的__________________(填“必要不充分”、“充分不必要”或“充要”)条件.
”的__________________(填“必要不充分”、“充分不必要”或“充要”)条件.
【原创】在整数集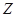 中,被5除所得余数为
中,被5除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为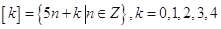 ,则下列结论正确的为
,则下列结论正确的为
①2015 ;②-1
;②-1 ;③
;③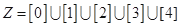 ;④命题“整数
;④命题“整数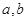 满足
满足 ,则
,则 ”的原命题与逆命题都正确;⑤“整数
”的原命题与逆命题都正确;⑤“整数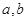 属于同一类”的充要条件是“
属于同一类”的充要条件是“ ”
”
已知p:(x-1)(y-2)=0,q:(x-1)2+(y-2)2=0,则p是q的________条件
下列四种说法:
①命题“ ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”;
②设 、
、 是简单命题,若“
是简单命题,若“ ”为假命题,则“
”为假命题,则“ ” 为真命题;
” 为真命题;
③若 是
是 的充分不必要条件,则
的充分不必要条件,则 的必要不充分条件;
的必要不充分条件;
④把函数
 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数
 的图像.
的图像.
其中所有正确说法的序号是 .
试题篮
()