某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是
 =-0.7x+
=-0.7x+ ,则
,则 = .
= .
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =bx+a.
=bx+a.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
设有一个直线回归方程为 ,则变量
,则变量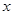 增加一个单位( )
增加一个单位( )
| A.y平均增加 1.5 个单位 |
| B.y 平均增加 2 个单位 |
| C.y 平均减少 1.5 个单位 |
| D.y 平均减少 2 个单位 |
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单元:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: =0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
=0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
某单位为了了解用电量y度与气温x0C之间的关系随机统计了某4天的用电量与当天气温
| 气温(0C) |
14 |
12 |
8 |
6 |
| 用电量 |
22 |
26 |
34 |
38 |
(1)求用电量y与气温x的线性回归方程;
(2)由(1)的方程预测气温为50C时,用电量的度数。
参考公式:
某地粮食需求量逐年上升,下表是部分统计数据:
| 年份(年) |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量 (万吨) |
236 |
246 |
257 |
276 |
286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程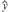 =
= x+
x+ .
.
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程,其中.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
设某中学的女生体重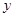 (kg)与身高
(kg)与身高 (cm)具有线性相关关系,根据一组样本数
(cm)具有线性相关关系,根据一组样本数
 ,用最小二乘法建立的线性回归直线方程为
,用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
A.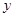 与 与 具有正的线性相关关系 具有正的线性相关关系 |
| B.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
C.回归直线至少经过样本数据  中的一个 中的一个 |
D.回归直线一定过样本点的中心点 |
A市积极倡导学生参与绿色环保活动,其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月(一年)内空气质量指数 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
| 指数API |
[0,50] |
(50,100] |
(100,150] |
(150,200] |
(200,250] |
(250,300] |
>300 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中重度污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
(1)若A市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数 (记为t)的关系
(记为t)的关系
为: ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成 列联表,并判断是
列联表,并判断是
否有 的把握认为A市本年度空气重度污染与供暖有关?
的把握认为A市本年度空气重度污染与供暖有关?
| |
非重度污染 |
重度污染 |
合计 |
| 供暖季 |
|
|
|
| 非供暖季节 |
|
|
|
| 合计 |
|
|
100 |
下面临界值表供参考.
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式: ,其中
,其中 .
.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前 吨甲产品能耗为
吨甲产品能耗为 吨标准煤;试根据(2)求出的线性回归方程,预测生产
吨标准煤;试根据(2)求出的线性回归方程,预测生产 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )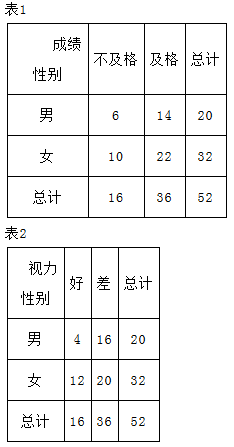
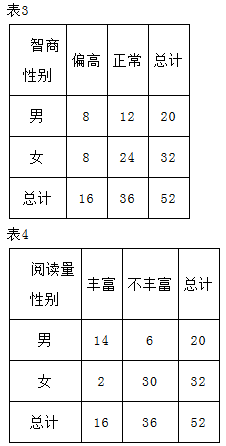
| A.成绩 | B.视力 | C.智商 | D.阅读量 |
下表数据是水温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的,且对于给定的x,y为变量.
| x(℃) |
300 |
400 |
500 |
600 |
700 |
800 |
| y(%) |
40 |
50 |
55 |
60 |
67 |
70 |
(1)求y关于x的回归方程;
(2)估计水温度是1 000 ℃时,黄酮延长性的情况.
(可能用到的公式: ,
, ,其中
,其中 、
、 是对回归直线方程
是对回归直线方程 中系数
中系数 、
、 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
试题篮
()