一名小学生的年龄和身高(单位:cm)的数据如下:
| 年龄X |
6 |
7 |
8 |
9 |
| 身高Y |
118 |
126 |
136 |
144 |
由散点图可知,身高y与年龄x之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A. 154 B. 153 C. 152 D. 151
若随机变量 服从两点分布,其中
服从两点分布,其中 ,则
,则 和
和 的值分别是( )
的值分别是( )
| A.4和4 | B.4和2 | C.2和4 | D.2和2 |
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
| A.y=-10x+200 | B.y=10x+200 |
| C.y=-10x-200 | D.y=10x-200 |
一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归直线方程为  ,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
| A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
已知边长为3的正方形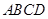 与正方形
与正方形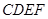 所在的平面互相垂直,
所在的平面互相垂直,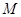 为线段
为线段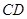 上的动点(不含端点),过
上的动点(不含端点),过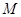 作
作 交
交 于
于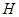 ,作
,作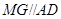 交
交 于
于 ,连结
,连结 .设
.设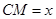
 ,则下面四个图象中大致描绘了三棱锥
,则下面四个图象中大致描绘了三棱锥 的体积
的体积 与变量
与变量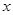 变化关系的是
变化关系的是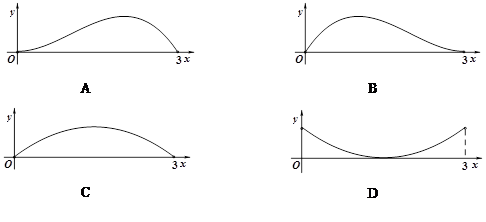
下列判断中不正确的是( )
A. 为变量间的相关系数, 为变量间的相关系数, 值越大,线性相关程度越高 值越大,线性相关程度越高 |
| B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律 |
C.线性回归方程代表了观测值 、 、 之间的关系 之间的关系 |
| D.任何一组观测值都能得到具有代表意义的回归直线方程 |
下列函数中,随x(x>0)的增大,增长速度最快的是( )
| A.y =1,x∈Z | B.y=x | C.y=  |
D.y=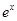 |
对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是 =
=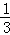 x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
A.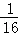 |
B.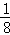 |
C.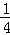 |
D. |
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间 与数学成绩
与数学成绩 进行数据收集如下:
进行数据收集如下:
| x |
15 |
16 |
18 |
19 |
22 |
| y |
102 |
98 |
115 |
115 |
120 |
由表中样本数据求得回归方程为 ,则点
,则点 与直线
与直线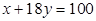 的位置关系是( )
的位置关系是( )
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
试题篮
()