设(x1,y1),(x2,y2), ,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是 ( )
A.直线l过点( , , ) ) |
| B.x和y的相关系数为直线l的斜率 |
| C.x和y的相关系数在0到1之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
线 性回归方程表示的直线
性回归方程表示的直线 必定
必定 过 ( )
过 ( )
| A.(0,0)点 | B.( ,0)点 ,0)点 |
C.( ,0)点 ,0)点 |
D.( , , )点 )点 |
设有一个回归直线方程 ,则变量x增加1个单位时
,则变量x增加1个单位时
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
某单位为了了解用电量 (千瓦时)与气温
(千瓦时)与气温 (
( )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温 ( ( ) ) |
18 |
13 |
10 |
 |
用电量 (千瓦时) (千瓦时) |
24 |
34 |
38 |
64 |
由表中数据得线性回归方程 中
中 ,预测当气温为
,预测当气温为 时,用电量约为( )
时,用电量约为( )
A.58千瓦时 B.66千瓦时 C.68千瓦时 D.70千瓦时
下面是两个变量的一组数据:
| X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
则这两个变量之间的线性回归方程是( )
A.y=-16+9x B.y=31-x C.y=30-x D.y=-15+9x
一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高 与年龄
与年龄 之间的线性回归方程为
之间的线性回归方程为 ,则
,则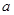 的值为( )
的值为( )
| A.65 | B.74 | C.56 | D.47 |
为了解某商品销售量 (单位:件)与销售价格
(单位:件)与销售价格 (单位:元/件)的关系,统计了(
(单位:元/件)的关系,统计了( )的10组值,并画成散点图如图,则其回归方程可能是
)的10组值,并画成散点图如图,则其回归方程可能是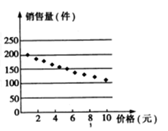
A. |
B.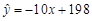 |
C.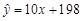 |
D. |
对于下列表格所示的五个散点,已知求得的线性回归直线方程为 =0.8x-155.
=0.8x-155.
| x |
196 |
197 |
200 |
203 |
204 |
| y |
1 |
3 |
6 |
7 |
m |
则实数m的值为( )
A.8.4 B.8.2 C.8 D.8.5
下列反映两个变量的相关关系中,不同于其它三个的是
| A.名师出高徒 | B.水涨船高 | C.月明星稀 | D.登高望远 |
若变量 与
与 之间的相关系数
之间的相关系数 ,则变量
,则变量 与
与 之间
之间
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
已知变量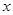 与
与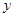 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,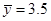 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.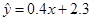 |
B.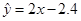 |
C.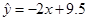 |
D.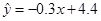 |
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程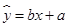 ,其中
,其中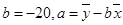 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
试题篮
()