在两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
| A.模型1的相关指数R2为0.98 | B.模型2的相关指数R2为0.90 |
| C.模型3的相关指数R2为0.60 | D.模型4的相关指数R2为0.25 |
在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是
A.若K2的观测值为k=6.635,而P(K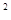 ≥6.635) =0.010,故我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 ≥6.635) =0.010,故我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 |
| B.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推断出现错误 |
| C.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病 |
| D.以上三种说法都不正确 |
设有一个回归方程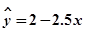 ,变量
,变量 增加一个单位时,变量
增加一个单位时,变量 平均
平均
A.减少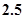 个单位 个单位 |
B.增加2个单位 |
C.增加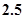 个单位 个单位 |
D.减少2个单位 |
某考察团对全国10大城市进行职工人均平均工资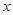 与居民人均消费
与居民人均消费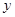 进行统计调查,
进行统计调查,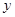 与
与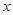 具有相关关系,回归方程
具有相关关系,回归方程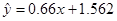 (单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
| A.66% | B.72.3% | C.67.3% | D.83% |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
对于线性回归方程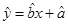 ,下列说法中不正确的是( )
,下列说法中不正确的是( )
A.直线必经过点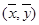 |
B.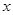 增加一个单位时, 增加一个单位时,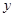 平均增加 平均增加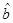 个单位 个单位 |
C.样本数据中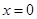 时,可能有 时,可能有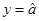 |
D.样本数据中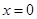 时,一定有 时,一定有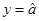 |
若用水量x与某种产品的产量y的回归方程是 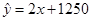 ,则当用水量为50kg时,预计的某种产品的产量是( )
,则当用水量为50kg时,预计的某种产品的产量是( )
| A.大于1350kg | B.小于 1350kg | C.1350kg | D.以上都不对 |
在一组样本数据 的散点图中,若所有样本点 都在直线 上,则这组样本数据的样本相关系数为()
| A. | -1 | B. | 0 | C. | D. | 1 |
已知x、y之间的一组数据如下:
| x |
0 |
1 |
2 |
3 |
| y |
8 |
2 |
6 |
4 |
则线性回归方程 所表示的直线必经过点( )
所表示的直线必经过点( )
A.(0,0) B.(1.5,5) C.(4,1.5) D.(2,2)
有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩;③某人每日吸烟量和其身体健康情况;
④正方形的边长和面积; ⑤汽车的重量和百公里耗油量;
其中两个变量成正相关的是( )
| A.①③ | B.②④ | C.②⑤ | D.④⑤ |
设某大学的女生体重 (单位: )与身高 (单位: )具有线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为 ,则下列结论中不正确的是
| A. | 与 具有正的线性相关关系 |
| B. | 回归直线过样本点的中心 |
| C. | 若该大学某女生身高增加1cm,则其体重约增加0.85kg |
| D. | 若该大学某女生身高为170cm,则可断定其体重比为58.79kg |
对于线性回归方程 ,下列说法中不正确的是( )
,下列说法中不正确的是( )
A.直线必经过点 |
B. 增加一个单位时, 增加一个单位时,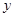 平均增加 平均增加 个单位 个单位 |
C.样本数据中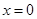 时,可能有 时,可能有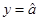 |
D.样本数据中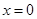 时,一定有 时,一定有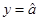 |
为了考察两个变量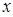 和
和 之间的线性相关性,甲、乙两位同学各自独立地做10次和15
之间的线性相关性,甲、乙两位同学各自独立地做10次和15
次试验,并且利用线性回归方法,求得回归直线分别为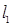 和
和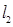 ,已知两个人在试验中发现对
,已知两个人在试验中发现对
变量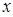 的观测数据的平均值都是
的观测数据的平均值都是 ,对变量
,对变量 的观测数据的平均值都是
的观测数据的平均值都是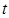 ,那么下列说法正
,那么下列说法正
确的是( )
A.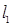 和 和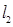 有交点( 有交点( , ,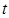 ) ) |
B.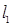 与 与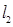 相交,但交点不一定是( 相交,但交点不一定是( , ,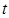 ) ) |
C.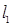 与 与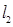 必定平行 必定平行 |
D.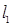 与 与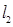 必定重合 必定重合 |
某种产品的广告费支出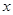 (单位:万元)与销售额
(单位:万元)与销售额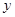 (单位:万元)之间的线性回归方程为
(单位:万元)之间的线性回归方程为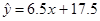 ,
,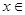 {2,4,5,6,8},则平均销售额
{2,4,5,6,8},则平均销售额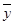 为( )
为( )
| A. 6.5 | B. 17.5 | C. 50 | D. 40 |
试题篮
()