一次兴趣调查,共调查了1000名学生,其中男女生各500名,喜欢数学的男260名,喜欢数学的女生有220名.
(1)根据以上数据作出2×2列联表
(2)运用独立性检验思想,判断喜欢数学与性别是否有关系?(要求达到99.9%才能认定为有关系)
参考数据与公式:
临界值表
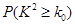 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知有线性相关关系的两个变量建立的回归直线方程为 ,方程中的回归系数
,方程中的回归系数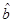 ( )
( )
| A.可以小于0 | B.只能大于0 | C.可以为0 | D.只能小于0 |
对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
| 月收入(单位百元) |
[15,25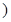 |
[25,35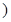 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
| |
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
| 赞成 |
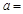 3 3 |
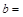 |
|
| 不赞成 |
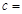 |
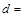 11 11 |
|
| 合计 |
|
|
50 |
(Ⅱ)若从月收入在[55,65)的被调查对象中随机选取两人进行调查,求至少有一人赞成“楼市限购政策”的概率.
(参考公式: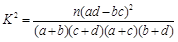 ,其中
,其中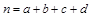 .)
.)
参考值表:
P(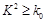 ) ) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
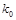 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
下面是对智商在40~69之间的人的出生季节所作的一项调查。结果如下(单位:人):
| 智商 季节 |
40~54 |
55~69 |
合计 |
| 夏和秋 |
20 |
30 |
50 |
| 春和冬 |
10 |
X |
50 |
| 合计 |
30 |
70 |
Y |
(Ⅰ) 请求出表中X和Y的值;
(Ⅱ) 问智商在40~69之间的人的智商与出生季节是否有关联?
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: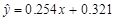 .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.
.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.
某产品的广告费用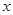 与销售额
与销售额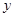 的统计数据如下表:
的统计数据如下表:
广告费用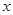 (万元) (万元) |
4 |
2 |
3 |
5 |
销售额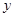 (万元) (万元) |
49 |
26 |
39 |
54 |
根据上表数据预计广告费用为6万元时,销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
某新型企业随市场竞争加剧,为获取更大利润,企业须不断加大投资,若预计年利润率低于10%时,则该企业就考虑转型.下表显示的是某企业几年来年利润 (百万)与年投资成本
(百万)与年投资成本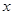 (百万)变化的一组数据.
(百万)变化的一组数据.
| 年份 |
2008 |
2009 |
2010 |
2011 |
… |
| 投资成本x |
3 |
5 |
9 |
17 |
… |
| 年利润y |
1 |
2 |
3 |
4 |
… |
请你就以下4个函数模型



其中以下说法
A. 年投资成本与年利润正相关
B. 选择其适合的函数模型是
C. 若要使企业利润超过6百万,则该企业考虑转型.
你认为正确的是 (把你认为正确的都填上)
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| |
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验:能否在犯错误的概率不超过0.01的前提下认为学生的学习积极性与对待班级工作的态度有关系?并说明理由. 附: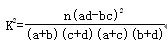
(参考下表)
| P(K2≥k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;(参考公式:b= ,
, )
)
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(参考数据:

 )
)
.(本小题满分12分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男生身高频数分布表
| 身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生身高频数分布表[来
| 身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
| 频数 |
1 |
7 |
12 |
6 |
3 |
1 |
(I)求该校男生的人数并完成下面频率分布直方图;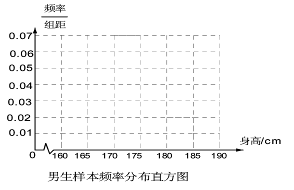
(II)估计该校学生身高在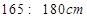 的概率;
的概率;
(III)从样本中身高在180 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185 190cm之间的概率。
190cm之间的概率。
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) |
2 |
4 |
5 |
6 |
8 |
| 每小时生产有缺点的零件数y(件) |
30 |
40 |
60 |
50 |
70 |
(1)画散点图
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值: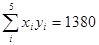 ,
, )
)
已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为y=bx+a必过点 D
A .(2,2) B.(1,2) C.(1.5,0) D (1.5,4)
下列两变量中不存在相关关系的是
①人的身高与视力;②曲线上的点与该点的坐标之间的关系;③某农田的水稻产量与施肥量;④某同学考试成绩与复习时间的投入量;⑤匀速行驶的汽车的行驶的距离与时间;⑥家庭收入水平与纳税水平;⑦商品的销售额与广告费.
| A.①②⑤ | B.①③⑦ | C.④⑦⑤ | D.②⑥⑦ |
在两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
| A.模型1的相关指数R2为0.98 | B.模型2的相关指数R2为0.90 |
| C.模型3的相关指数R2为0.60 | D.模型4的相关指数R2为0.25 |
试题篮
()