高中数学变量间的相关关系试题

下表是某厂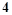～月份用水量（单位：百吨）的一组数据：

月份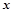
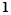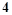用水量

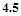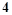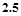由散点图可知，用水量与月份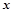之间有较好的线性相关关系，其线性回归直线方程是，则据此模型预测6月份用水量为________百吨

.三点（3，10），（7，20）,(11,24)的回归方程是

A．y=5-17x	B．y=-17+5x
C． y=17+5x	D． y=17-5x

.设有一个回归方程y=3-5x则变量x增加一个单位时

A．y平均减少5个单位	B．y平均增加3个单位.
C．y平均减少3个单位	D．y平均增加5个单位.

某种产品的广告费支出与销售额ｙ之间的（单位：百万元）之间的有如下对应数据：

	2	4	5	6	8
	30	40	60	50	70

y与x之间的线性回归方程为，则=                   

.在下列各图中，每个图的两个变量具有相关关系的图是（   ）
       
        （1）             （2）         （3）          （4）

A．（1）（2）

B．（1）（3）

C．（2）（4）

D．（2）（3）

有五组变量：①汽车的重量和汽车每消耗1升汽油所行驶的平均路程；
②平均日学习时间和平均学习成绩；   ③某人每日吸烟量和其身体健康情况；
④正方形的边长和面积；             ⑤汽车的重量和百公里耗油量；
其中两个变量成正相关的是     （   ）

A．①③

B．②④

C．②⑤

D．④⑤

下列关系中，具有相关关系的是（   ）

A．人的身高与体重；	B．匀速行驶的车辆所行驶距离与行驶的时间；
C．人的身高与视力；	D．正方体的体积与边长.

.某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表：

月平均气温x（）	17	13	8	2
月销售量y（件）	24	33	40	55

由表中数据算出线性回归方程中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为_ 件.
(参考公式：)

一台机器使用的时候较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：

转速χ（转/秒）	16	14	12	8
每小时生产有缺点的零件数y（件）	11	9	8	5

 
（1）画出散点图，并通过散点图确定变量y对χ是否线性相关；
（2）如果y对χ有线性相关关系，求回归直线方程；
（3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？（精确到0.0001）
参考公式：线性回归方程的系数公式：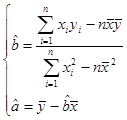

在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的=20.87，根据这一数据分析，我们有_______的把握认为打鼾与患心脏病是______ 的.

．对相关系数r，下列说法正确的是 (      )

A．越大，线性相关程度越大

B．越小，线性相关程度越大

C．越大，线性相关程度越小，越接近0，线性相关程度越大

D．且越接近1，线性相关程度越大，越接近0，线性相关程度越小

下表是x与y之间的一组数据，则y关于x的线性回归直线必过点(    )

x	0	1	2	3
y	1	3	5	7

 
A.(2,2)       B.(1.5,2)    C.(1,2)       D.(1.5,4)

对四组数据进行统计，获得以下散点图，关于其线性相关系数比较，正确的是（  ）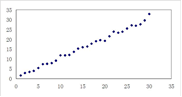
     
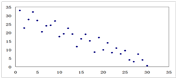
线性相关系数为                 线性相关系数为
     
线性相关系数为                 线性相关系数为

A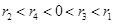．	B．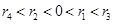
C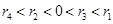．	D．

下表是某厂1～4月份用水量（单位：百吨）的一组数据，

月份	1	2	3	4
用水量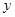	4.5	4	3	2.5

由其散点图可知，用水量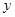与月份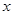之间有较好的线性相关关系，其线性回归方程是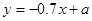，则=______________。

已知x,y的取值如下表所示：

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7. 0

从散点图可以看出x与y线性相关.
（1）求出线性回归方程.
（2）请估计x=10时y的值.
参考数据与公式：