某单位为了制定节能减排目标,先调查了用电量 (单位:度)与气温
(单位:度)与气温 (单位:
(单位: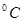 )之间的关系,随机统计了某
)之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表:
天的用电量与当天气温,并制作了对照表:
 |
 |
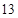 |
 |
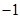 |
||||
 |
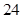 |
 |
 |
 |
||||
由表中数据,得线性回归直线方程 ,当气温不低于
,当气温不低于 时,预测用电量最多为 度.
时,预测用电量最多为 度.
已知具有线性相关的两个变量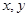 之间的一组数据如下:
之间的一组数据如下:
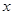 |
0 |
1 |
2 |
3 |
4 |
 |
2.2 |
4.3 |
4.5 |
4.8 |
6.7 |
且回归方程是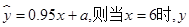 的预测值为( )
的预测值为( )
A.8.1 B.8.2 C.8.3 D.8.4
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: .由回归直线方程可知,
.由回归直线方程可知,
家庭年收入每增加1万元,年饮食支出平均增加____________万元;
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的
列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由 算得,
算得,
附表:
 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论是( )
A、有99%以上的把握认为“爱好该项运动与性别有关”
B、有99%以上的把握认为“爱好该项运动与性别无关”
C、在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别有关”
D、在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别无关”
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列
由 算得,
算得,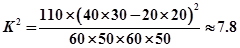 .
.
参照附表,得到的正确结论是 ( )
| A.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” |
| B.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” |
| C.有99%以上的把握认为“爱好该项运动与性别有关” |
| D.有99%以上的把握认为“爱好该项运动与性别无关” |
对于两个变量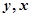 进行回归分析时,分别选择了4个模型,它们的相关指数
进行回归分析时,分别选择了4个模型,它们的相关指数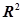 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1,相关指数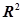 为0.89 为0.89 |
B.模型2,相关指数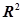 为0.98 为0.98 |
C.模型3,相关指数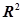 为0.09 为0.09 |
D.模型4,相关指数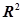 为0.50 为0.50 |
已知某校5个学生的数学和物理成绩如下表
(1)假设在对这 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少?
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用 表示数学成绩,用
表示数学成绩,用 表示物理成绩,求
表示物理成绩,求 与
与 的回归方程;
的回归方程;
(3)利用残差分析回归方程的拟合效果,若残差和在 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
参考数据和公式: ,其中
,其中 ,
, ;
; ,残差和公式为:
,残差和公式为:
某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据:由资料显示 对
对 呈线性相关关系。
呈线性相关关系。
根据上表提供的数据得到回归方程 中的
中的 ,预测销售额为115万元时约需
,预测销售额为115万元时约需
万元广告费.
某校的研究性学习小组为了研究中学生的身高与性别情况,在该校随机抽出80名17至18周岁的学生,其中身高 的男生有30人,女生4人;身高<170的男生有10人。
的男生有30人,女生4人;身高<170的男生有10人。
(1)根据以上数据建立一个 列联表:
列联表:
(2)请问在犯错误的概率不超过0.001的前提下,该校17至18周岁的学生的身高与性别是否有关?
参考公式: 
参考数据: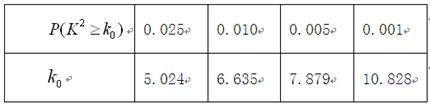
某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考数值: )
)
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
| 年份200x(年) |
0 |
1 |
2 |
3 |
4 |
| 人口数y(十万) |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求最小二乘法求出y关于x的线性回归方程y=bx+a;
(3) 据此估计2012年.该 城市人口总数.
(参考数值:0×5+1×7+2×8+3×11+4×19=132, ,公式见卷首)
,公式见卷首)
我校开展研究性学习活动,高二某同学获得一组实验数据如下表:
| x |
1.99 |
3 |
4 |
5.1 |
6.12 |
| y |
1.5 |
4.04 |
7.5 |
12 |
18.01 |
对于表中数据,现给出以下拟合曲线,其中拟合程度最好的是
A.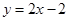 B.
B. C.
C.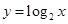 D.
D.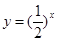
试题篮
()