有关线性回归的说法,不正确的是( )
| A.相关关系的两个变量不是因果关系 |
| B.散点图能直观地反映数据的相关程度 |
| C.回归直线最能代表线性相关的两个变量之间的关系 |
| D.任一组数据都有回归方程 |
(本小题满分13分)某同学大学毕业后在一家公司上班,工作年限 和年收入
和年收入 (万元),有以下的统计数据:
(万元),有以下的统计数据:
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(Ⅲ)请你估计该同学第8年的年收入约是多少?
(参考公式: )
)
(本小题10分)某种产品的广告费用支出 与销售额
与销售额 之间有如下的对应数据:
之间有如下的对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
50 |
60 |
70 |
(1)求 对
对 的回归直线方程;
的回归直线方程;
(2)据此估计广告费用为10销售收入 的值.
的值.
参考公式:
下表是某工厂1~4月份用电量(单位:万度)的一组数据:
月份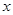 |
1 |
2 |
3 |
4 |
用电量 |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用电量 与月份
与月份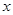 间有较好的线性相关关系,其线性回归直线方程是
间有较好的线性相关关系,其线性回归直线方程是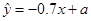 ,则
,则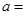 ( )
( )
A.10.5 B.5.25 C.5.2 D.5.15
经统计,某地的财政收入 与支出
与支出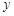 满足的线性回归模型是
满足的线性回归模型是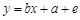 (单位:亿元),其中
(单位:亿元),其中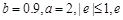 为随机误差,如果今年该地区财政收入10亿元,则年支出预计不超出( )
为随机误差,如果今年该地区财政收入10亿元,则年支出预计不超出( )
| A.10亿 | B.11亿 | C.11.5亿 | D.12亿 |
某考察团对全国10大城市进行职工人均平均工资 与居民人均消费
与居民人均消费 进行统计调查,
进行统计调查,  与
与 具有相关关系,回归方程
具有相关关系,回归方程 (单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
| A.66% | B.72.3% |
| C.67.3% | D.83% |
某产品广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归直线方程 中的
中的 为9.4,据此模型预报广告费用为6万元时销售额为 .
为9.4,据此模型预报广告费用为6万元时销售额为 .
某研究小组为了研究中学生的身体发育情况,在某学校随机抽出20名15至16周岁的男生,将他们的身高和体重制成2×2的列联表,根据列联表的数据,可以有 %的把握认为该学校15至16周岁的男生的身高和体重之间有关系.
| |
超重 |
不超重 |
合计 |
| 偏高 |
4 |
1 |
5 |
| 不偏高 |
3 |
12 |
15 |
| 合计 |
7 |
13 |
20 |
下表是某厂1-4月份用水量(单位:100t)的一组数据, 由其散点图可知, 用水量y与月份x之间有较好的线性相关关系,其线性回归方程是_________________.
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y(100t) |
4.4 |
4 |
3 |
2.5 |
一位母亲记录了她的儿子3~9岁的身高数据,并由此建立身高与年龄的回归模型为y=7.19x+73.93,用这个模型预测她的儿子10岁时的身高,则正确的叙述是
| A.身高一定是145.83 cm | B.身高在145.83 cm以上 |
| C.身高在145.83 cm左右 | D.身高在145.83 cm以下 |
.已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程y=bx+a必过点 (填写序号)
①(2,2) ②(1.5,0) ③(1.5,4) ④ (1, 2)
某产品的广告费用 与销售额
与销售额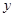 的统计数据如下表:
的统计数据如下表:
广告费用 (万元) (万元) |
4 |
2 |
3 |
5 |
销售额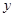 (万元) (万元) |
49 |
26 |
39 |
54 |
根据以上表可得回归方程 中的
中的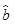 为
为 据此模型预报广告费用为
据此模型预报广告费用为 万元时销售额为( )
万元时销售额为( )
A.63.6万元 B. 65.5万元 C.67.7万元 D.72.0万元
如果散点图中所有的样本点均在同一条直线上,那么残差平方和与相关系数分别为 ( )
| A.1,0 | B.0,1 | C.0.5,0.5 | D.0.43,0.57 |
下面是一个2×2列联表: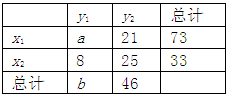
则表中a、b处的值分别为 ( )
| A.94、96 | B.52、50 | C.52、60 | D.54、52 |
试题篮
()