某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
请画出上表数据的散点图; (要求 : 点要描粗)
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: )
)
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分 |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在图的直角坐标系中作出这些数据的散点图,并求出这些数据的同归方程;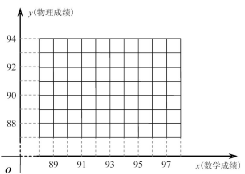
(2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值.
给出以下四个说法:
①在匀速传递的产品生产流水线上,质检员每间隔 分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
②在刻画回归模型的拟合效果时,相关指数 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量 平均增加
平均增加 个单位;
个单位;
④对分类变量 与
与 ,若它们的随机变量
,若它们的随机变量 的观测值
的观测值 越小,则判断“
越小,则判断“ 与
与 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是
| A.①④ | B.②④ | C.①③ | D.②③ |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是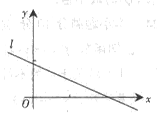
| A. x;和y正相关 |
| B. x和y的相关系数为直线l的斜率 |
| C. x和y的相关系数在-1到0之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线Z是由这些样本点通过 最小二乘法得到的线性回归方程(如图),以下结论中正确的是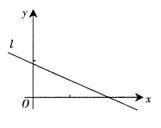
| A.x;和y正相关 |
| B.y和y的相关系数为直线I的斜率 |
| C.x和y的相关系数在-1到O之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
某工厂在2004年的各月中,一产品的月总成本y(万元)与月产量x(吨)之间有如下数据:
| X |
4.16 |
4.24 |
4.38 |
4.56 |
4.72 |
4.96 |
5.18 |
5.36 |
5.6 |
5.74 |
5.96 |
6.14 |
| Y |
4.38 |
4.56 |
4.6 |
4.83 |
4.96 |
5.13 |
5.38 |
5.55 |
5.71 |
5.89 |
6.04 |
6.25 |
若2005年1月份该产品的计划产量是6吨,试估计该产品1月份的总成本.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据 收集到的数据(如下表),由最小二乘法求得回归直线方程

表中有一个数据模糊不清,请你推断出该数据的值为______ .
设有一个线性回归直线方程为 ,则变量
,则变量 每增加一个单位时( )
每增加一个单位时( )
A. 平均增加 1.5 个单位 平均增加 1.5 个单位 |
B. 平均增加 2 个单位 平均增加 2 个单位 |
C. 平均减少 1.5 个单位 平均减少 1.5 个单位 |
D. 平均减少 2 个单位 平均减少 2 个单位 |
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了 至
至 月份每月
月份每月 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
昼夜温差 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
6 |
就诊人数 (个) (个) |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取 组,用剩下的
组,用剩下的 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的 组数据进行检验.
组数据进行检验.
(Ⅰ)求选取的 组数据恰好是相邻两个月的概率;
组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是 月与
月与 月的两组数据,请根据
月的两组数据,请根据 至
至 月份的数据,求出
月份的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;(其中
;(其中 )
)
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过 人,则认为得到的线性回归方程是理想的.试问该小组所得线性回归方程是否理想?
人,则认为得到的线性回归方程是理想的.试问该小组所得线性回归方程是否理想?
已知某产品的广告费用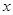 万元与销售额
万元与销售额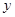 万元的统计数据如表所示:
万元的统计数据如表所示:
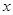 (万元) (万元) |
0 |
1 |
3 |
4 |
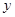 (万元) (万元) |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析,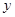 与
与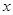 线性相关,且
线性相关,且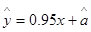 ,则据此模型预报广告费用为6万元时销售额为
,则据此模型预报广告费用为6万元时销售额为
A. 2.6万元 B. 8.3万元 C. 7.3万元 D. 9.3万元
已知统计某产品的广告费用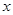 (万元)与销售额
(万元)与销售额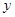 (万元)所得的数据如下表所示:
(万元)所得的数据如下表所示:
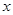 |
0 |
1 |
3 |
4 |
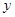 |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析,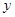 与
与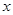 有较强的线性相关性,且
有较强的线性相关性,且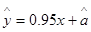 ,则
,则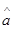 等于
等于
A. 2.6万元 B. 2.4万元 C. 2.7万元 D. 2.5万元
一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
| A.身高一定是145.83cm | B.身高在145.83cm以上 |
| C.身高在145.83cm以下 | D.身高在145.83cm左右 |
下表是某厂1~4月份用水量(单位:百吨)的一组数据,
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是y=-0.7x+a,则a=____ __.
试题篮
()