以下是某地搜集到的新房屋的销售价格 和房屋的面积
和房屋的面积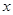 的数据:
的数据:
房屋面积 |
110 |
90 |
80 |
100 |
120 |
| 销售价格(万元) |
33 |
31 |
28 |
34 |
39 |
(1)画出数据对应的散点图;
(2)求线性回归方程;
(3)据(2)的结果估计当房屋面积为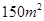 时的销售价格.
时的销售价格.
(提示: ,
,  ,
, ,
, )
)
某市居民1999~2003年货币收入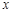 与购买商品支出
与购买商品支出 的统计资料如下表所示:单位:亿元
的统计资料如下表所示:单位:亿元
| 年份 |
1999 |
2000 |
2001 |
2002 |
2003 |
货币收入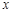 |
40 |
42 |
44 |
47 |
50 |
购买商品支出 |
33 |
34 |
36 |
39 |
41 |
(Ⅰ)画出散点图,判断x与Y是否具有相关关系;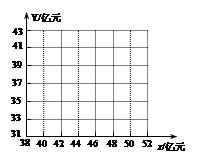
(Ⅱ)已知 ,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
在独立性检验中,统计量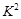 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当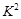 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当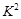 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当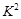
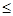 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的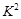 =20.87,根据这一数据分析,认为打鼾与患心脏病之间
=20.87,根据这一数据分析,认为打鼾与患心脏病之间
| A.有95%的把握认为两者有关 | B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 | D.约有99%的打鼾者患心脏病 |
下列说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系; |
B.线性回归方程对应的直线 = = x+ x+ 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; |
| C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高; |
D.在回归分析中, 为0.98的模型比 为0.98的模型比 为0.80的模型拟合的效果好. 为0.80的模型拟合的效果好. |
某工厂的某种型号的机器的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)有下表的统计资料:
(万元)有下表的统计资料:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
根据上表可得回归方程 ,据此模型估计,该型号机器使用年限为10年时维修费用约 万元(结果保留两位小数).
,据此模型估计,该型号机器使用年限为10年时维修费用约 万元(结果保留两位小数).
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 |
A |
B |
C |
D |
E |
销售额 (千万元) (千万元) |
3 |
5 |
6 |
7 |
9 9 |
利润额 (百万元) (百万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额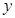 关于销售额
关于销售额 的回归直线方程;
的回归直线方程;
(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
给出下列命题:
①线性回归方程 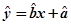 必过
必过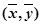 ;
;
②函数 的零点有2个;
的零点有2个;
③函数 的图象与
的图象与 轴围成的图形面积是
轴围成的图形面积是 ;
;
④函数 是偶函数,且在区间
是偶函数,且在区间 内单调递增;
内单调递增;
⑤函数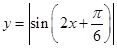 的最小正周期为
的最小正周期为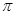 .其中真命题的序号是 。
.其中真命题的序号是 。
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
 |
文艺节目 |
新闻节目 |
总计 |
| 20~40岁 |
40 |
18 |
58 |
| 大于40岁 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(1) 由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应抽取几名?
对变量 有观测数据
有观测数据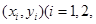 …,10),得散点图(1)所示.对变量
…,10),得散点图(1)所示.对变量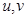 有观测数据
有观测数据 ,…,10),得散点图(2).由这两个散点图可以判断
,…,10),得散点图(2).由这两个散点图可以判断
A.变量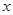 与 与 正相关, 正相关,  与 与 正相关 正相关 |
B.变量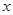 与 与 正相关, 正相关,  与 与 负相关 负相关 |
C.变量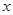 与 与 负相关, 负相关,  与 与 正相关 正相关 |
D.变量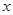 与 与 负相关, 负相关,  与 与 负相关 负相关 |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 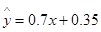 ,那么表中m的值为( )
,那么表中m的值为( )
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
m |
4 |
4.5 |
A. 4 B. 3.5 C. 4.5 D. 3
(本小题12分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: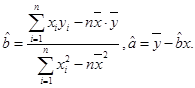 )
)
实验测得四组 的值分别为
的值分别为 ,则y关于x的线性回归方程必过点( )
,则y关于x的线性回归方程必过点( )
| A.(2,8) | B.(2.5,8) |
| C.(10,31) | D.(2.5,7.75) |
某地区恩格尔系数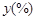 与年份
与年份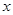 的统计数据如下表:
的统计数据如下表:
年份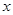 |
2004 |
2005 |
2006 |
2007 |
恩格尔系数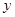 (%) (%) |
47 |
45.5 |
43.5 |
41 |
从散点图可以看出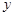 与
与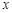 线性相关,且可得回归直线方程为
线性相关,且可得回归直线方程为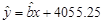 ,据此模型可预测2013年该地区的恩格尔系数(%)为 .
,据此模型可预测2013年该地区的恩格尔系数(%)为 .
试题篮
()