高中数学变量间的相关关系试题

已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是(   )

A．=1.23x＋4

B．=1.23x+5

C．=1.23x+0.08

D．=0.08x+1.23

两个变量有线性相关关系且正相关，则回归直线方程中，的系数（　）　

A．

B．

C．

D．

在如下图所示的各图中，两个变量具有相关关系的是(　　)

A．(1)(2)	B．(1)(3)
C．(2)(4)	D．(2)(3)

设有一个直线回归方程为y=2-1.5x,则变量x增加一个单位时  （  ）

A．y平均增加1.5个单位	B．y平均增加2个单位
C．y平均减少1.5个单位	D．y平均减少2个单位

下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨
标准煤)的几组对照数据：

(1)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产
l00吨甲产品的生产能耗比技改前降低多少吨标准煤?
（参考数值：3×2.5+4×3+5×4+6×4.5="66.5"  
用最小二乘法求线性回归方程系数公式）.

若样本+2，+2， ，+2的平均数为10，方差为3，则样本2+3，2+3，… ，2+3，
的平均数、方差、标准差是（   ）

A．19，12，

B．23，12，

C．23，18，

D．19，18，

某产品的广告费用x与销售额y的统计数据如下表

广告费用x（万元）	4	2	3	5
销售额y（万元）	49	26	39	54

根据上表可得回归方程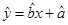中的为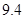，据此模型预报广告费用为7万元时销售额（   ）
A．63．6万元   B．65．5万元   C．77．9万元   D．74．9万元

变量x，y有观测数据(x_i，y_i)(i＝1,2，，10)，得散点图(1)；对变量u，v有观测数据( u_i，
v_i)(i ＝1,2，，10)，得散点图(2)．由这两个散点图可以判断．
 

A．变量x与y正相关，u与v正相关

B．变量x与y正相关，u与v负相关

C．变量x与y负相关，u与v正相关

D．变量x与y负相关，u与v负相关

为了解目前老年人居家养老还是在敬老院养老的意向，共调查了50名老年人，其中男性明确表示去敬老院养老的有5人，女性明确表示居家养老的有10人，已知在全部50人中随机地抽取1人明确表示居家养老的概率为。
（1）请根据上述数据建立一个2×2列联表；
（2）居家养老是否与性别有关？请说明理由。
参考公式：
参考数据：

	0.100	0.050	0.025	0.010	0.001
	2.706	3.841	5.024	6.635	10.828

下列选项中，两个变量具有相关关系的是(　　)

A．正方形的面积与周长	B．匀速行驶车辆的行驶路程与时间
C．人的身高与体重	D．人的身高与视力

对变量 有观测数据（，）（），得散点图1；对变量有观测数据（，）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断

A．变量x 与y 正相关，u 与v 正相关	B．变量x 与y 正相关，u 与v 负相关
C．变量x 与y 负相关，u 与v 正相关	D．变量x 与y 负相关，u 与v 负相关

在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人。女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个2×2的列联表；
（2）判断性别与休闲方式是否有关系。
附：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

某种产品的广告费用支出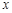与销售额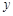之间有如下的对应数据：

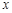	2	4	5	6	8
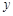	30	40	60	50	70

则回归直线方程为                 

在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的如下，其中拟合效果最好的模型是（     ）

A．模型1的为0.975	B．模型2的为0.79
C．模型3的为0.55	D．模型4的为0.25

某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了 5次试验.根据收集到的数据(如下表），由最小二乘法求得回归方程

现发现表中有一个数据模糊看不清，请你推断出该数据的值为______