下列两个变量之间的关系是相关关系的是 ( )
| A.正方体的棱长和体积 | B.单位圆中角的度数和所对弧长 |
| C.单产为常数时,土地面积和总产量 | D.日照时间与水稻的亩产量 |
对变量 有观测数据理力争 ,得散点图1;对变量 有观测数据 ,得散点图2. 由这两个散点图可以判断 ()

| A. | 变量 与 正相关, 与 正相关 | B. | 变量 与 正相关, 与 负相关 |
| C. | 变量 与 负相关, 与 正相关 | D. | 变量 与 负相关, 与 负相关 |
下列两个变量之间的关系哪个不是函数关系:
| A.圆的半径和该圆的周长 | B.角度和它的正弦值 |
| C.人的年龄和他的身高 | D.正多边形的边数和它的内角和 |
在线性回归模型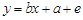 中,下列说法正确的是 ( )
中,下列说法正确的是 ( )
A.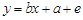 是一次函数; 是一次函数; |
B.因变量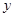 是由自变量 是由自变量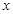 唯一确定的; 唯一确定的; |
C.因变量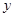 除了受自变量 除了受自变量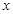 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差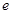 的产生; 的产生; |
D.随机误差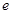 是由于计算不准确造成的,可以通过精确计算避免随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差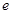 的产生. 的产生. |
某防疫站对屠宰场及肉食零售点的猪肉检查沙门氏菌带菌情况,结果如下表,试检查屠宰场与零售点猪肉带菌有无差异
| |
带菌头数 |
不带菌头数 |
合计 |
| 屠宰场 |
8 |
32 |
40 |
| 零售店 |
14 |
18 |
32 |
| 合计 |
22 |
50 |
72 |
( )
)
经过对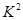 的统计量的研究,得到了若干个临界值,当
的统计量的研究,得到了若干个临界值,当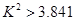 时,我们
时,我们
A.有95%的把握认为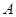 与 与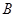 有关. 有关. |
B.有99%的把握认为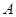 与 与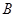 有关 有关 |
C.没有充分理由说事件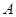 与 与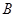 有关 有关 |
D.有97.5%的把握认为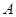 与 与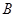 有关 有关 |
某种产品的广告费用支出 万元与销售额
万元与销售额 万元之间有如下的对应数据:
万元之间有如下的对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
20 |
30 |
50 |
50 |
70 |
(1)根据上表提供的数据,求出y关于x的线性回归方程;
(2)据此估计广告费用为10万元时,所得的销售收入.
( ,
,
 )
)
为了调查胃病是否与生活规律有关,在某地对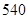 名
名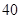 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共 人,患胃病者生活规律的共
人,患胃病者生活规律的共 人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共
人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共 人.
人.
(1)根据以上数据列出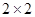 列联表.
列联表.
(2)并判断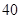 岁以上的人患胃病与否和生活规律是否有关。
岁以上的人患胃病与否和生活规律是否有关。
一家新技术公司计划研制一个名片管理系统,希望系统能够具备以下功能:
(1)用户管理:能修改密码,显示用户信息,修改用户信息。
(2)用户登录。
(3)名片管理:能够对名片进行删除、添加、修改、查询。
(4)出错信息处理。
请根据这些要求画出该系统的结构图.
已知每一吨铸铁成本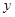 (元)与铸件废品率
(元)与铸件废品率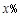 建立的回归方程
建立的回归方程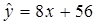 ,下列说法正确的是( )
,下列说法正确的是( )
A.废品率每增加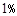 ,平均每吨成本增加64元 ,平均每吨成本增加64元 |
B.废品率每增加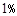 ,平均每吨成本增加 ,平均每吨成本增加 |
C.废品率每增加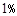 ,平均每吨成本增加8元 ,平均每吨成本增加8元 |
D.废品率每增加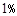 ,平均每吨成本为56元 ,平均每吨成本为56元 |
对于给定的两个变量的统计数据,下列说法正确的是 ( )
| A.都可以分析出两个变量的关系 | B.都可以用一条直线近似地表示两者的关系 |
| C.都可以作出散点图 | D.都可以用确定的表达式表示两者的关系 |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
由表中数据算的线性回归方程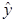 =bx+a中的b≈0.7,试预测加工10个零件需小时数为( )。(已知
=bx+a中的b≈0.7,试预测加工10个零件需小时数为( )。(已知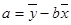 )
)
A、9 B、8.5 C、8.05 D、8
甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验,并用回归分析方法分别求得相关系数r与残差平方和m如下表;则哪位同学的试验结果体现A、B两变量更强的线性相关性
A.丁 B.丙 C.乙 D.甲
| |
甲 |
乙 |
丙 |
丁 |
| r |
0.82 |
0.78 |
0.69 |
0.85 |
| m |
115 |
106 |
124 |
103 |
观察两相关量得如下数据:求两变量间的回归直线方程 .
| x |
-1 |
-2 |
-3 |
-4 |
-5 |
5 |
3 |
4 |
2 |
1 |
| y |
-9 |
-7 |
-5 |
-3 |
-1 |
1 |
5 |
3 |
7 |
9 |
试题篮
()