某商店经营一批进价为每件4元的商品,在市场调查时得到,此商品的销售单价x与日销售量y之间的一组数据满足: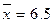 ,
, ,
,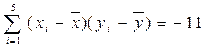 ,
, ,则当销售单价x定为(取整数) 元时,日利润最大.
,则当销售单价x定为(取整数) 元时,日利润最大.
下列命题中正确的为 .(填上你认为正确的所有序号)
(1)用更相减损术求295和85的最大公约数时,需要做减法的次数是12;
(2)利用语句X=A,A=B,B=X可以实现交换变量A,B的值;
(3)用秦九韶算法计算多项式 在
在 时的值时,
时的值时, 的值为
的值为 ;
;
(4)如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变。
某产品的广告费用x与销售额y的统计数据如下表
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39[ |
54 |
根据上表可得回归方程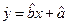 中的
中的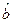 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
A.63.6万元 B.65.5万元 C.67.7万元 D
D .72.0万元
.72.0万元
一项研究要确定是否能够根据施肥量预测作物的产量。这里的预报释变量是( )
| A.作物的产量 | B.施肥量 |
| C.试验者 | D.降雨量或其他解释产量的变量 |
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由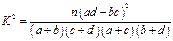 算得,
算得,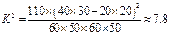 .
.
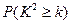 |
0.050 |
0.010 |
0.001 |
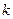 |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论是( )
A.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
若由资料可知y对x呈线性相关关系,则y与x的线性回归方程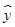 =bx+a必过的点是
=bx+a必过的点是
| A.(2,2) | B.(1,2) | C.(3,4) | D.(4,5) |
已知变量 呈线性相关关系,回归方程为
呈线性相关关系,回归方程为 ,则变量
,则变量 是( )
是( )
| A.线性正相关关系 | B.由回归方程无法判断其正负相关 |
| C.线性负相关关系 | D.不存在线性相关关系 |
(本小题满分13分)
某种产品的广告费支出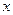 与销售额
与销售额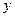 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
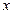 |
2 |
4 |
5 |
6 |
8 |
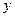 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的
绝对值不超过5的概率。
(参考数据: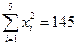
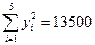
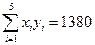 ,
,
参考公式:回归直线方程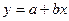 ,其中
,其中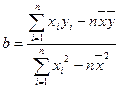 )
)
(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测:生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考公式: ,其中
,其中 )
)
.以下是粤西地区某县搜集到的新房屋的销售价格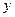 和
和 房屋的面积
房屋的面积 的数据:
的数据: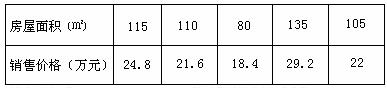
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为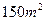 时的销售价格。
时的销售价格。
参考公式: 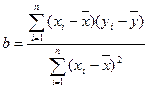 ,
,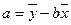
参考数据: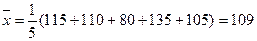 ,
,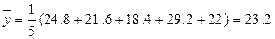
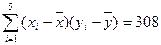 ,
,
容量为100的样本数据,按从小到大的顺序分为8组,如下表:
第三组的频数和频率分别是 ( )
A. 和0.14 和0.14 |
B.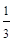 和 和 |
C.14和0.14 | D.0.14和14 |
某医疗研究所为了检 验某种血清预防
验某种血清预防 感冒的作用,把500名使用血清的人与另外500名未使用血清的人的一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”。对此利用2×2列联表计算得χ2≈3.918,经查对临界值表知P(χ2≥3.841)≈0.05。对此四名同学做出了如下的判断:
感冒的作用,把500名使用血清的人与另外500名未使用血清的人的一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”。对此利用2×2列联表计算得χ2≈3.918,经查对临界值表知P(χ2≥3.841)≈0.05。对此四名同学做出了如下的判断:
①有95%的把握认为“这种血清能起到预防感冒的作用”;②如果某人未使用该血清,那么他在一年中有95%的可能性得感冒;③这种血清预防感冒的有效率为95%; ④这种血清预防感冒的有效率为5%;
其中判断正确的序号是 。
试题篮
()