(本小题满分12分)
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
昼夜温差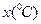 |
10 |
11 |
13 |
12 |
8 |
6 |
就诊人数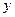 个 个 |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
⑴求选取的2组数据恰好是相邻两个月的概率;
⑵若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出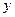 关于
关于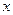 的线性回归方程
的线性回归方程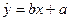 ;
;
⑶若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
则根据表中的数据,计算随机变量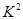 的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
A.0 B.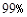 C .99.5% D.
C .99.5% D.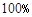
某医疗研究所为了检验某种血清预防感冒的作用,把 名使用血清的人与另外
名使用血清的人与另外 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设 :“这种血清不能起到预防感
:“这种血清不能起到预防感 冒的作用”,利用
冒的作用”,利用 列联表计算得
列联表计算得 ,经查对临界
,经查对临界 值表知
值表知 .对此,四名同学做出了以下的判断:
.对此,四名同学做出了以下的判断: :有
:有 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用” :若某人未使用该血清,那么他在一年中有
:若某人未使用该血清,那么他在一年中有 的可能性得感冒
的可能性得感冒 :这种血清预防感冒的有效率为
:这种血清预防感冒的有效率为
 :这种血清预
:这种血清预 防感冒的有效率为
防感冒的有效率为
则下列结论中,正确结论的序号是
①  ; ②
; ② ; ③
; ③ ; ④
; ④
调查某医院某段时间内婴儿出生的时间与性别的关系,由 列联表得出
列联表得出 ,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
A. |
B. |
C. |
D. |
(本小题满分12分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2列联表;
(2)判断休闲方式与性别是否有关。
(参考公式:
参考数据: )
)
为研究变量 的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
得到回归直线方程 ,两人计算知
,两人计算知 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
A. 重合 重合 |
B. 一定平行 一定平行 |
C. |
D.无法判断 是否相交 是否相交 |
在一次实验中,采集到如下一组数据:
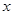 |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
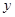 |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则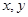 的函数关系与下列( )类函数最接近(其中
的函数关系与下列( )类函数最接近(其中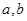 为待定系数)
为待定系数)
A.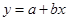 B .
B .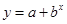 C.
C.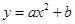 D.
D.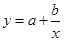
有五组变量:
①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩;
③某人每日吸烟量和其身体健康情况;
④正方形的边长和面积; 
⑤汽车的重量和百公里耗油量;
其中两个变量成正相关关系的是
| A.①③ | B.②④ | C.②⑤ | D.④⑤ |
已知 的取值如下表所示:
的取值如下表所示:
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析, 与
与 线性相关,且
线性相关,且 ,则
,则 _______________
_______________
某产品的广告费用
与销售额
的统计数据如下表:
| 广告费用
(万元) |
4 |
2 |
3 |
5 |
| 销售额
(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程
中的
为9.4,据此模型预报广告费用为6万元时销售额为
| A. | 63.6万元 |
B. | 65.5万元 |
C. | 67.7万元 |
D. | 72.0万元 |
调查在2~3级风时的海上航行中男女乘客的晕船情况,共调查了71人,其中女性34人,男性37人。女性中有10人晕船,另外24人不晕船;男性中有12人晕船,另外25人不晕船。
判断晕船是否与性别有关系。
若某地财政收入x与支出y满足线性回归方程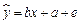 (单位:亿元),其中b=0.8,a=2,|e|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
(单位:亿元),其中b=0.8,a=2,|e|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
| A.10亿元 | B.9亿元 | C.10.5亿元 | D.9.5亿元 |
(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| |
甲流水线 |
乙流水线 |
合 计 |
| 合格品 |
a= |
b= |
|
| 不合格品 |
c= |
d= |
|
| 合 计 |
|
|
n= |
试题篮
()