在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:

参照附表,下列结论正确的是( ).
A.在犯错误的概率不超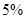 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; |
B.在犯错误的概率不超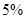 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; |
C.有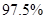 的把握认为“小动物是否被感染与有没有服用疫苗有关”; 的把握认为“小动物是否被感染与有没有服用疫苗有关”; |
D.有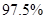 的把握认为“小动物是否被感染与有没有服用疫苗无关”. 的把握认为“小动物是否被感染与有没有服用疫苗无关”. |
(本小题满分12分)
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得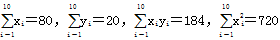 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,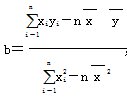 ,a=
,a= -b
-b 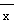 ,其中
,其中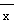 ,
, 为样本平均值.
为样本平均值.
某次测量发现一组数据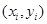 具有较强的相关性,并计算得
具有较强的相关性,并计算得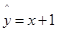 ,其中数据
,其中数据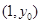 ,Y)因书写不清,只记得
,Y)因书写不清,只记得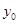 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是
 =-0.7x+
=-0.7x+ ,则
,则 = .
= .
下表数据是水温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的,且对于给定的x,y为变量.
| x(℃) |
300 |
400 |
500 |
600 |
700 |
800 |
| y(%) |
40 |
50 |
55 |
60 |
67 |
70 |
(1)求y关于x的回归方程;
(2)估计水温度是1 000 ℃时,黄酮延长性的情况.
(可能用到的公式: ,
, ,其中
,其中 、
、 是对回归直线方程
是对回归直线方程 中系数
中系数 、
、 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
| 时间 |
油耗(升/100公里) |
可继续行驶距离(公里) |
| 10:00 |
9.5 |
300 |
| 11:00 |
9.6 |
220 |
注: ,
,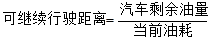 ,
,
 .
.
从以上信息可以推断在10:00—11:00这一小时内 (填上所有正确判断的序号).
行驶了80公里;
行驶不足80公里;
平均油耗超过9.6升/100公里;
平均油耗恰为9.6升/100公里;
平均车速超过80公里/小时.
对变量 ,
,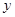 观测数据
观测数据 ,得散点图
,得散点图 ;对变量
;对变量 ,
, 有观测数据
有观测数据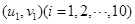 ,得散点图
,得散点图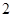 .由这两个散点图可以判断( )
.由这两个散点图可以判断( )

A.变量 与 与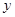 正相关, 正相关, 与 与 正相关 正相关 |
B.变量 与 与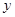 正相关, 正相关, 与 与 负相关 负相关 |
C.变量 与 与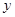 负相关, 负相关, 与 与 正相关 正相关 |
D.变量 与 与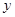 负相关, 负相关, 与 与 负相关 负相关 |
生产 ,
, 两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |
 |
 |
 |
 |
 |
元件 |
8 |
12 |
40 |
32 |
8 |
元件 |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计元件 、元件
、元件 为正品的概率;
为正品的概率;
(Ⅱ)生产一件元件 ,若是正品可盈利50元,若是次品则亏损10元;生产一件元件
,若是正品可盈利50元,若是次品则亏损10元;生产一件元件 ,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下
,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下
(i)求生产5件元件 所获得的利润不少于300元的概率;
所获得的利润不少于300元的概率;
(ii)记 为生产1件元件
为生产1件元件 和1件元件
和1件元件 所得的总利润,求随机变量
所得的总利润,求随机变量 的分布列和期望.
的分布列和期望.
欲知作者的性别是否与读者的性别有关,某出版公司派人员到各书店随机调查了500位买书的顾客,结果如下:
| 作家 读者 |
男作家 |
女作家 |
合计 |
| 男读者 |
142 |
122 |
264 |
| 女读者 |
103 |
133 |
236 |
| 合计 |
245 |
255 |
500 |
则作者的性别与读者的性别 (填“有关”或“无关”)。
通过随机询问110名大学生是否爱好某项运动,得到如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由上表算得k≈7.8,因此得到的正确结论是( )
| P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
2015年,各大品牌汽车继续在中国的汽车市场上相互博弈,汽车的配置与销售价格以及维修费用等成为人们购买汽车时需要考虑的因素,某汽车制造商为了进一步拓宽市场,统计了某种品牌的汽车的使用年限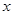 和所支出的维修费用
和所支出的维修费用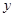 (万元),得到的统计资料:
(万元),得到的统计资料:
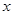 |
2 |
3 |
4 |
5 |
6 |
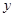 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知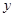 对
对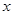 呈线性相关关系,且线性回归方程为
呈线性相关关系,且线性回归方程为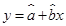 ,其中已知
,其中已知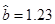 ,根据国家政策规定,轿车取消报废年限,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为_________.
,根据国家政策规定,轿车取消报废年限,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为_________.
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程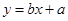 ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
| y |
4.0 |
2.5 |
 0.5 0.5 |
0.5 |
 2.0 2.0 |
得到的回归方程为 .若
.若 ,则
,则 每增加1个单位,
每增加1个单位, 就( ).
就( ).
A.增加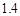 个单位 B.减少
个单位 B.减少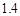 个单位
个单位
C.增加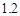 个单位 D.减少
个单位 D.减少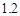 个单位
个单位
A市积极倡导学生参与绿色环保活动,其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月(一年)内空气质量指数 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
| 指数API |
[0,50] |
(50,100] |
(100,150] |
(150,200] |
(200,250] |
(250,300] |
>300 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中重度污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
(1)若A市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数 (记为t)的关系
(记为t)的关系
为: ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成 列联表,并判断是
列联表,并判断是
否有 的把握认为A市本年度空气重度污染与供暖有关?
的把握认为A市本年度空气重度污染与供暖有关?
| |
非重度污染 |
重度污染 |
合计 |
| 供暖季 |
|
|
|
| 非供暖季节 |
|
|
|
| 合计 |
|
|
100 |
下面临界值表供参考.
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式: ,其中
,其中 .
.
试题篮
()